
How do you solve \[{x^3} - 3{x^2} - x + 3 = 0\]?
Answer
547.2k+ views
Hint: Here in this question, the given equation in the form of a cubic equation with x has a variable. This equation can be solved by using factor theorem or synthetic division. First find the one root by a guesswork or trial and error method and write the quadratic equation by using the method of synthetic equation and further simplify the quadratic equation by factorization for finding other two roots.
Complete step-by-step solution:
A cubic function or equation is a third-degree polynomial. A general polynomial function has the form: \[f(x) = a{x^n} + b{x^{n - 1}} + c{x^{n - 2}}...v{x^3} + w{x^2} + zx + k\]
Here, x is the variable, n is simply any number (and the degree of the polynomial), k is a constant and the other elements or letters are constant coefficients for each power of x. so a cubic function has n=3, and is simply: \[f(x) = a{x^3} + b{x^2} + c{x^1} + d\]
The easiest way to solve a cubic equation involves a bit of guesswork and an algorithmic type of process called synthetic division. Though it is basically the same as the trial-and-error method for cubic equation solutions.
Consider the given cubic equation
\[ \Rightarrow \,\,\,{x^3} - 3{x^2} - x + 3 = 0\]
Try to find one of the roots by guessing.
You have to guess one of the values of x, let the first factor be \[x = 1\], then
\[ \Rightarrow \,\,\,{1^3} - 3{\left( 1 \right)^2} - 1 + 3 = 0\]
\[ \Rightarrow \,\,\,1 - 3 - 1 + 3 = 0\]
\[ \Rightarrow \,\,\,0 = 0\]
This means x=1 is a root of the cubic equation. You can get the answer without much thought and it is also time-consuming (especially if you have to go to higher factors before finding a root). Luckily, when you’ve found one root, you can solve the rest of the equation easily. The key is incorporating the factor theorem. This states that if x = s is a solution, then (x – s) is a factor that can be pulled out of the equation. For this situation, s = 1, and so (x-1) is a factor.
Next find the quadratic equation by the method of synthetic division. First, write down the coefficients of the original or given equation in the first row of a table, with a dividing line and then the known root on the right:
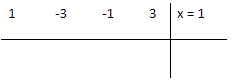
Leave one spare row, and then add a horizontal line below it. First, take the first number (1 in this case) down to the row below your horizontal line
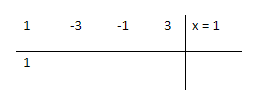
Continue the steps of synthetic division
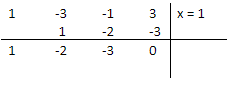
The fact that the last answer is zero tells you that you’ve got a valid root, so if this isn’t zero, then you’ve made a mistake somewhere.
Now, the bottom row tells you the factors of the three terms in the second set of brackets, so the cubic equation is written as:
\[ \Rightarrow \,\,\left( {x - 1} \right)\left( {{x^2} - 2x - 3} \right) = 0\]
This is the most important stage of the solution, and you can finish from this point onwards by factorization. this is basically the same problem as factoring a quadratic equation.
Consider the quadratic equation present in second bracket
\[ \Rightarrow \,\,\,{x^2} - 2x - 3\]
Now, break the middle term as the summation of two numbers such that its product is equal to -3. Calculated above such two numbers are 1 and -3.
\[ \Rightarrow \,\,\,{x^2} + 1x - 3x - 3\]
Making pairs of terms in the above expression
\[ \Rightarrow \,\,\,\left( {{x^2} + x} \right) - \left( {3x + 3} \right)\]
Take out greatest common divisor GCD from the both pairs, then
\[ \Rightarrow \,\,\,x\left( {x + 1} \right) - 3\left( {x + 1} \right)\]
Take \[\left( {x + 1} \right)\] common
\[ \Rightarrow \,\,\,\left( {x + 1} \right)\left( {x - 3} \right)\]
Therefore, factors of cubic equations are
\[ \Rightarrow \,\,\left( {x - 1} \right)\,\left( {x + 1} \right)\left( {x - 3} \right)\]
To find the roots by equate each factor to the zero then
\[ \Rightarrow \,\,\left( {x - 1} \right) = 0\]
\[\therefore \,\,\,\,x = 1\]
\[ \Rightarrow \,\,\left( {x + 1} \right) = 0\]
\[\therefore \,\,\,\,x = - 1\]
\[ \Rightarrow \,\,\left( {x - 3} \right) = 0\]
\[\therefore \,\,\,\,x = 3\]
Hence, the roots of the given cubic equation \[{x^3} - 3{x^2} - x + 3 = 0\] is 1, -1 and 3.
Note: The cubic equation contains 3 roots. To find or solve the cubic equation, solved by using the synthetic division method. The one value or root of the given equation determined by the synthetic division. Then the quadratic equation will remain, to the quadratic equation the sum product rule or by standard formula is applied to determine the other two roots
Complete step-by-step solution:
A cubic function or equation is a third-degree polynomial. A general polynomial function has the form: \[f(x) = a{x^n} + b{x^{n - 1}} + c{x^{n - 2}}...v{x^3} + w{x^2} + zx + k\]
Here, x is the variable, n is simply any number (and the degree of the polynomial), k is a constant and the other elements or letters are constant coefficients for each power of x. so a cubic function has n=3, and is simply: \[f(x) = a{x^3} + b{x^2} + c{x^1} + d\]
The easiest way to solve a cubic equation involves a bit of guesswork and an algorithmic type of process called synthetic division. Though it is basically the same as the trial-and-error method for cubic equation solutions.
Consider the given cubic equation
\[ \Rightarrow \,\,\,{x^3} - 3{x^2} - x + 3 = 0\]
Try to find one of the roots by guessing.
You have to guess one of the values of x, let the first factor be \[x = 1\], then
\[ \Rightarrow \,\,\,{1^3} - 3{\left( 1 \right)^2} - 1 + 3 = 0\]
\[ \Rightarrow \,\,\,1 - 3 - 1 + 3 = 0\]
\[ \Rightarrow \,\,\,0 = 0\]
This means x=1 is a root of the cubic equation. You can get the answer without much thought and it is also time-consuming (especially if you have to go to higher factors before finding a root). Luckily, when you’ve found one root, you can solve the rest of the equation easily. The key is incorporating the factor theorem. This states that if x = s is a solution, then (x – s) is a factor that can be pulled out of the equation. For this situation, s = 1, and so (x-1) is a factor.
Next find the quadratic equation by the method of synthetic division. First, write down the coefficients of the original or given equation in the first row of a table, with a dividing line and then the known root on the right:
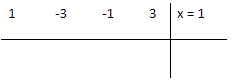
Leave one spare row, and then add a horizontal line below it. First, take the first number (1 in this case) down to the row below your horizontal line
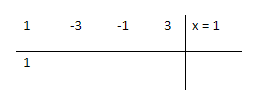
Continue the steps of synthetic division
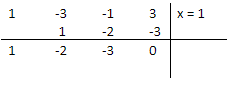
The fact that the last answer is zero tells you that you’ve got a valid root, so if this isn’t zero, then you’ve made a mistake somewhere.
Now, the bottom row tells you the factors of the three terms in the second set of brackets, so the cubic equation is written as:
\[ \Rightarrow \,\,\left( {x - 1} \right)\left( {{x^2} - 2x - 3} \right) = 0\]
This is the most important stage of the solution, and you can finish from this point onwards by factorization. this is basically the same problem as factoring a quadratic equation.
Consider the quadratic equation present in second bracket
\[ \Rightarrow \,\,\,{x^2} - 2x - 3\]
Now, break the middle term as the summation of two numbers such that its product is equal to -3. Calculated above such two numbers are 1 and -3.
\[ \Rightarrow \,\,\,{x^2} + 1x - 3x - 3\]
Making pairs of terms in the above expression
\[ \Rightarrow \,\,\,\left( {{x^2} + x} \right) - \left( {3x + 3} \right)\]
Take out greatest common divisor GCD from the both pairs, then
\[ \Rightarrow \,\,\,x\left( {x + 1} \right) - 3\left( {x + 1} \right)\]
Take \[\left( {x + 1} \right)\] common
\[ \Rightarrow \,\,\,\left( {x + 1} \right)\left( {x - 3} \right)\]
Therefore, factors of cubic equations are
\[ \Rightarrow \,\,\left( {x - 1} \right)\,\left( {x + 1} \right)\left( {x - 3} \right)\]
To find the roots by equate each factor to the zero then
\[ \Rightarrow \,\,\left( {x - 1} \right) = 0\]
\[\therefore \,\,\,\,x = 1\]
\[ \Rightarrow \,\,\left( {x + 1} \right) = 0\]
\[\therefore \,\,\,\,x = - 1\]
\[ \Rightarrow \,\,\left( {x - 3} \right) = 0\]
\[\therefore \,\,\,\,x = 3\]
Hence, the roots of the given cubic equation \[{x^3} - 3{x^2} - x + 3 = 0\] is 1, -1 and 3.
Note: The cubic equation contains 3 roots. To find or solve the cubic equation, solved by using the synthetic division method. The one value or root of the given equation determined by the synthetic division. Then the quadratic equation will remain, to the quadratic equation the sum product rule or by standard formula is applied to determine the other two roots
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




