Question

How do you solve for $x$ in $3x+y=7$?

Answer 1

Hint: Change of form of the given equation will give the x-intercept and y-intercept of the line $3x+y=7$. As there is only one equation to solve two unknowns, we will get an infinite number of solutions. We change the equation to the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$ to find the x intercept, and y intercept of the line as $p$ and $q$ respectively. Then we place the points on the axes and from there we draw the line on the graph. All the points on the line are solutions for $x$ in $3x+y=7$.

Complete step-by-step answer:
We are taking the general equation of line to understand the slope and the intercept form of the line $3x+y=7$. We have to find the x-intercept, and y-intercept of the line $3x+y=7$.
For this we convert the given equation into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$. From the form we get that the x intercept, and y intercept of the line will be$p$ and $q$ respectively. The points will be $\left( p,0 \right),\left( 0,q \right)$. The given equation is $3x+y=7$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$
$\begin{align}
  & 3x+y=7 \\
 & \Rightarrow \dfrac{3x}{7}+\dfrac{y}{7}=1 \\
 & \Rightarrow \dfrac{x}{{}^{7}/{}_{3}}+\dfrac{y}{7}=1 \\
\end{align}$
Therefore, the x intercept, and y intercept of the line $3x+y=7$ is $\dfrac{7}{3}$ and 7 respectively. The axes intersecting points are $\left( \dfrac{7}{3},0 \right),\left( 0,7 \right)$. These two values of $x=\dfrac{7}{3},0$ are two solutions of an infinite number of solutions.

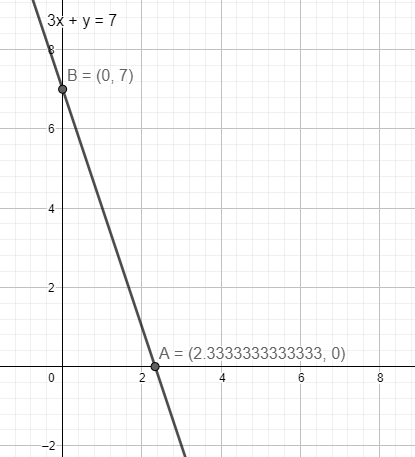
Note: A line parallel to the X-axis does not intersect the X-axis at any finite distance. Hence, we cannot get any finite x-intercept of such a line. Same goes for lines parallel to the Y-axis. In case of slope of a line the range of the slope is 0 to $\infty $.