Question

How do you solve $ 2{{e}^{x}}=10 $ ?

Answer 1

Hint: The equation given in the question is an exponential equation. We know that if we are given an equation like $ {{e}^{x}}=y $ the x will be equal to $ \ln y $ . We can write y in terms of x. We can solve the question by using a logarithm.

Complete step by step answer:
The given equation in the question is $ 2{{e}^{x}}=10 $ .
If we further solve the equation we will get
 $ \Rightarrow {{e}^{x}}=5 $
Now we know that if y is equal to $ {{e}^{x}} $ then x will be equal to $ \ln y $ . That means $ \ln x $ is the inverse function of $ {{e}^{x}} $ .We can write $ \ln \left( {{e}^{x}} \right)=x $ and $ {{e}^{\ln x}}=x $
So by applying the above statement to our equation we get
 $ x=\ln 5 $
We can find the value of $ \ln 5 $ by using a logarithm table. The value of $ \ln 5 $ is equal to 1.609. If n is a rational number then $ \ln \left( n \right) $ will always be irrational so $ \ln 5 $ is an irrational number, we can not write its actual value. We can write its approximate value by using log tale.
The value of x is $ \ln 5 $ which is approximately 1.609.

Note:
 Another method to solve the equation is by drawing the graph. To solve $ 2{{e}^{x}}=10 $ we can write $ {{e}^{x}}=5 $ we can draw the graph of $ y={{e}^{x}} $ and $ y=5 $ then the intersection point of these 2 curves will be our solution, but here also we can not find the proper actual answer we can find the approximate value
The graph of $ y={{e}^{x}} $ and $ y=5 $

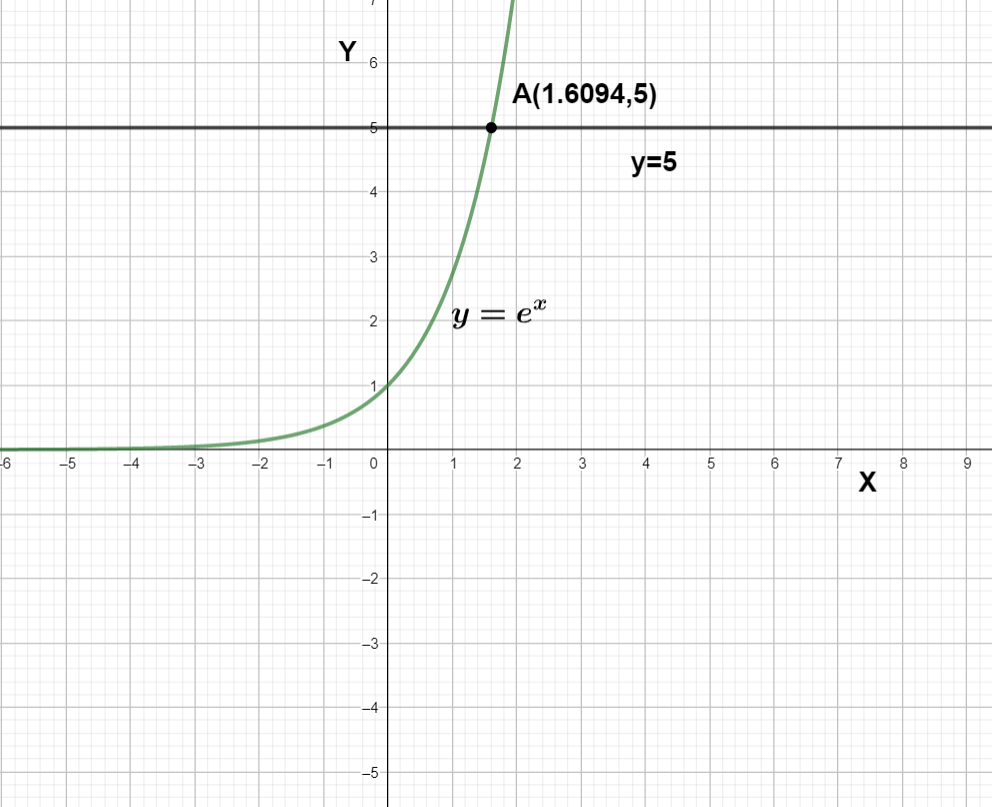
We can see the green curve is $ y={{e}^{x}} $ and the black one is $ y=5 $ the intersection point is A(1.6094,5). So the value of x from the graph is 1.6094 which is approximately equal to $ \ln 5 $.