Question

How do you graph $y=\sqrt{x-1}$?

Answer 1

Hint: We equate the given equation of parabolic curve with the general equation of ${{\left( y-\beta \right)}^{2}}=4a\left( x-\alpha \right)$. We find the number of x intercepts and the value of the y intercept. We also find the coordinates of the focus to place the curve in the graph. The given equation is also the positive part of y. We explain the situation for only the positive part.

Complete step by step answer:
The given equation $y=\sqrt{x-1}$ is a parabolic curve. Squaring both sides of the equation, we get ${{y}^{2}}=x-1$. But due to taking the extra negative side of the y part, we have to omit the negative part at the end.
We equate ${{y}^{2}}=x-1$ with the general equation of parabola ${{\left( y-\beta \right)}^{2}}=4a\left( x-\alpha \right)$.
For the general equation $\left( \alpha ,\beta \right)$ is the vertex. 4a is the length of the latus rectum. The coordinate of the focus is $\left( \alpha +a,\beta \right)$.
Now we convert the given equation $y=\sqrt{x-1}$ according to the general equation to find the value of the vertex.
We get
$\begin{align}
  & {{y}^{2}}=x-1 \\
 & \Rightarrow {{\left( y-0 \right)}^{2}}=\left( x-1 \right) \\
\end{align}$
This gives the vertex as $\left( 1,0 \right)$. The length of the latus rectum is $4a=1$ which gives $a=\dfrac{1}{4}$.

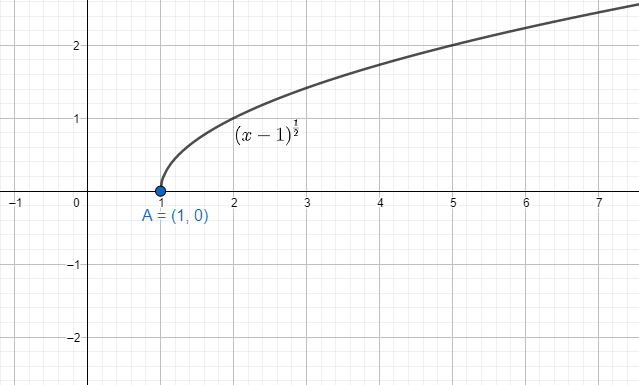
We have to find the possible number of x intercepts and the value of the y intercept. The curve cuts the X and Y axis at certain points and those are the intercepts.
We first find the Y-axis intercepts. In that case for the Y-axis, we have to take the coordinate values of x as 0. Putting the value of $x=0$ in the equation $y=\sqrt{x-1}$, we get
$y=\sqrt{0-1}$
There is no such value of y for which x will be 0. The curve never touches the Y-axis.
We first find the X-axis intercepts. In that case for X-axis, we have to take the coordinate values of y as 0. Putting the value of $y=0$ in the equation $y=\sqrt{x-1}$, we get
\[\begin{align}
  & y=\sqrt{x-1} \\
 & \Rightarrow 0=\sqrt{x-1} \\
 & \Rightarrow x=1 \\
\end{align}\]
The intercept points are $\left( 1,0 \right)$. There is only one intercept on the X-axis and that point is the vertex.

Note: The minimum point of the function $y=\sqrt{x-1}$ is $y=0$. The graph is bounded at that point. But on the other side the curve is open and not bounded. The general case of parabolic curve is to be bounded at one side to mark the vertex.