Question

How do you graph $y = \sin 4x - 4\sin x$?

Answer 1

Hint: Since this graph is quite complex in the sense that we do not know any of its property, we will try to plot a few points of it find its periodicity and then with help of a graphing calculator see what the graph actually looks like. The first task ahead of us would be to find the periodicity of the given graph, since both of the term of the expression
$y = \sin 4x - 4\sin x$
Will have different periods, the lcm of the period of both the graphs will be the period of the compound oscillation of this graph , we will keep that in mind . The period of the $\sin 4x$ will be $\dfrac{\pi }{2}$ while the period of $4\sin x$ or particularly $\sin x$ since $4$ is constant will be $2\pi $ as it is a sine function we will find the lcm and get value of the period of complete function, then put few points to get our values.

Complete step by step solution:
The given function,
$y = \sin 4x - 4\sin x$
Is a complex function, we have to first find periodicity . The period of the $\sin 4x$ will be $\dfrac{\pi }{2}$while the period of $4\sin x$ or particularly $\sin x$ since $4$ is constant will be $2\pi $ as it is a sine function we will find the lcm and get value of the period of complete function the lcm will be $2\pi $and hence the period will be $2\pi $.
Also we put few values and get the corresponding value the function gives,
Lets put $ - \pi ,\pi , - 2\pi ,2\pi $,
We get \[ - 4.0,{\text{ }}4.0,{\text{ }} - 2.0,{\text{ }}2.0\]
We will put these values to plot a graph we will now see the graph from a calculator,

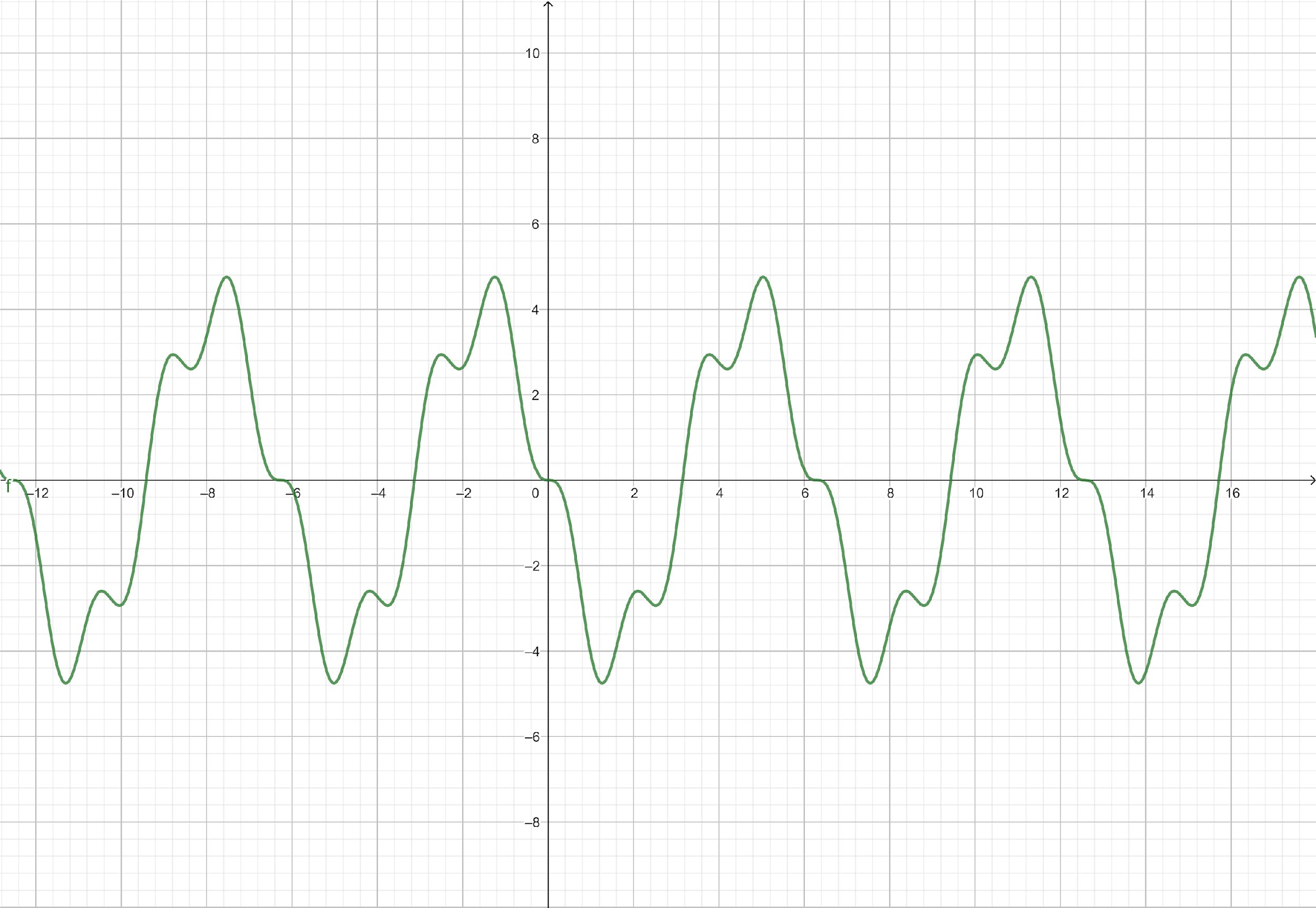
Note:
If a complex function is given then the period will be the LCM of periodicity all the terms in that given function.