
How do you graph \[x - y = 10\]\[?\]
Answer
558k+ views
Hint: The given question describes the arithmetic operation of addition/ subtraction/ multiplication/ division. We need to know how to find the value of \[y\] from the above equation. Also, this problem involves substituting \[x\] values in the given equation to find the value \[y\]. By using \[x\] and \[y\] values we would draw the graph.
Complete step by step solution:
The given equation is shown below,
\[x - y = 10\]
The above equation can also be written as,
\[y = x - 10 \to \left( 1 \right)\]
We would draw the graph for the above equation. As a first step, we would assume \[x\] values as given below,
\[x = ..... - 2, - 1,0,1,2,.....\]
By substituting the \[x\] values in the equation \[\left( 1 \right)\], we can find the \[y\] values.
Let’s substitute \[x = - 2\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = - 2 - 10 \\
y = - 12 \\
\]
When \[x = - 2\] the value of \[y\] is \[ - 12\]
Let’s substitute \[x = - 1\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = - 1 - 10 \\
y = - 11 \\
\]
When \[x = - 1\] the value of \[y\] is \[ - 11\]
Let’s substitute \[x = 0\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = 0 - 10 \\
y = - 10 \\
\]
When \[x = 0\] the value of \[y\] is \[ - 10\]
Let’s substitute \[x = 1\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = 1 - 10 \\
y = - 9 \\
\]
When \[x = 1\] the value of \[y\] is \[ - 9\]
Let’s substitute \[x = 2\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = 2 - 10 \\
y = - 8 \\
\]
When \[x = 2\] then the value of \[y\] is \[ - 8\]
Let’s make a tabular column by using the \[x\] and \[y\] values.
By using these points we can easily draw the graph,
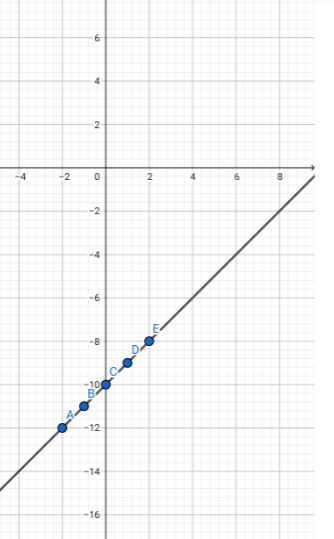
The above graph represents the equation \[y = x - 10\]
Note: \[y\] is the function of \[x\] so it can also be written as \[f\left( x \right)\]. Also, this type of question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. For finding the value of \[y\] point we can assume the \[x\] values. Note that if an equation is in the form of \[y = mx + c\], the graph always will be a straight line.
Complete step by step solution:
The given equation is shown below,
\[x - y = 10\]
The above equation can also be written as,
\[y = x - 10 \to \left( 1 \right)\]
We would draw the graph for the above equation. As a first step, we would assume \[x\] values as given below,
\[x = ..... - 2, - 1,0,1,2,.....\]
By substituting the \[x\] values in the equation \[\left( 1 \right)\], we can find the \[y\] values.
Let’s substitute \[x = - 2\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = - 2 - 10 \\
y = - 12 \\
\]
When \[x = - 2\] the value of \[y\] is \[ - 12\]
Let’s substitute \[x = - 1\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = - 1 - 10 \\
y = - 11 \\
\]
When \[x = - 1\] the value of \[y\] is \[ - 11\]
Let’s substitute \[x = 0\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = 0 - 10 \\
y = - 10 \\
\]
When \[x = 0\] the value of \[y\] is \[ - 10\]
Let’s substitute \[x = 1\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = 1 - 10 \\
y = - 9 \\
\]
When \[x = 1\] the value of \[y\] is \[ - 9\]
Let’s substitute \[x = 2\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = x - 10\]
\[
y = 2 - 10 \\
y = - 8 \\
\]
When \[x = 2\] then the value of \[y\] is \[ - 8\]
Let’s make a tabular column by using the \[x\] and \[y\] values.
| \[x\] | \[ - 2\] | \[ - 1\] | \[0\] | \[1\] | \[2\] |
| \[y\] | \[ - 12\] | \[ - 11\] | \[ - 10\] | \[ - 9\] | \[ - 8\] |
By using these points we can easily draw the graph,

The above graph represents the equation \[y = x - 10\]
Note: \[y\] is the function of \[x\] so it can also be written as \[f\left( x \right)\]. Also, this type of question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. For finding the value of \[y\] point we can assume the \[x\] values. Note that if an equation is in the form of \[y = mx + c\], the graph always will be a straight line.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

Which are the Top 10 Largest Countries of the World?

Draw ray diagrams each showing i myopic eye and ii class 12 physics CBSE

Giving reasons state the signs positive or negative class 12 physics CBSE

Explain esterification reaction with the help of a class 12 chemistry CBSE

What is defined as a solenoid Depict a diagram with class 12 physics CBSE




