Question

How do you graph $|x+y|>1$?

Answer 1

Hint: Inequality is a condition applied to an expression. To solve an inequality means to find the range of the values of the variable such that inequality holds through. Perform some suitable mathematical operations on both the sides and find the condition on b.

Complete step by step solution:
The given above is an inequality in terms of a variable x and y. Therefore, let us first understand what is meant by an inequality.
As the same suggests, inequality refers to something (say some variable) being not exactly equal to something. In other words, we can say that the value of the quantity is not exactly known but we do know some restriction or condition for the value of the quantity.
For example, suppose we have a stick in our hand and we want to measure the length of that stick. However, we do not have any measuring instrument to measure its length. Now, we approximate the length of the stick and we surely know that the stick cannot be more than one metre (by using some other stick whose length is exactly one metre).
Here, the length (L) of the stick is unknown but it is true that the length is less than one metre.
i.e. L < 1m
The given inequality says that $|x+y|>1$.
Here, $|x+y|>1$ is always a positive value and the inequality says that it must be greater than 1.
If x and y are both positive, then the inequality will be $x+y>1$
Therefore, the region that satisfies the above inequality is above the line $x+y=1$.

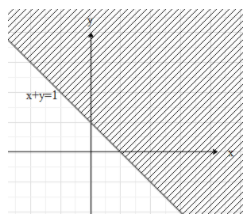
If x and y are both negative, then the inequality will be $-(x+y)>1\Rightarrow x+y<-1$
Therefore, the region that satisfies the above inequality is below the line $x+y-1$.

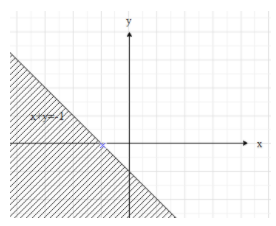
Now, if we merge the two graphs, then we get the final graph for the given inequality.
i.e.

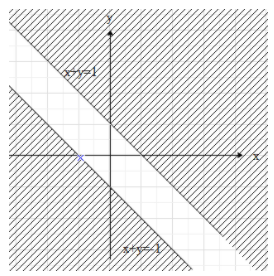
Note:
Note that the solution of an inequality is also an inequality and not a particular value of the variable.
Note that when multiplying or dividing a negative number on both the sides of the inequality, the sign of the operator changes. This means that the less than operator becomes greater than operator and vice versa.