Question

How do you graph the line $y = 2$?

Answer 1

Hint:
The general form of the equation of the straight line is $ax + by + c = 0$ and the given equation is $y = 2$ . Compare both the equations to get the value of ‘a’, ‘b’, and ‘c’. Now find the solution of ‘x’ and ‘y’ and plot the graph of the line.

Complete Step by step Solution:
Here in this problem, we are given an equation of the line, i.e. $y = 2$ and we need to graph this line in the coordinate plane.
The general form of the equation of the line is given as $ax + by + c = 0$ , where ‘x’ and ‘y’ are the coordinates of the x-axis and y-axis, and ‘a’, ’b’ and ‘c’ are the numbers, typically present in the simplified form of integers.
Here, in this case, we are given the equation:
$ \Rightarrow y = 2{\text{ or }}y - 2 = 0$
Now we can compare the equation $ax + by + c = 0$ with $y - 2 = 0$ . This will give us:
$ \Rightarrow b = 1,c = - 2{\text{ and }}a = 0$
So now we can represent the given equation using these values as:
$ \Rightarrow y - 2 = 0 \Rightarrow 0 \times x + 1 \times y - 2 = 0$
In the equation $y = 2$ , the coordinate of ‘y’ satisfies only one value, which is given as:
$ \Rightarrow {\text{ For }}y = 2$ , the equation will be: $y - 2 = 2 - 2 = 0$ , which satisfies the equation
Therefore, there exists only one value that can be attained by y-coordinate.
For x-coordinate, in the equation $0 \times x + 1 \times y - 2 = 0$ , we can put any value of ‘x’
\[ \Rightarrow {\text{ For }}x = 1;{\text{ }}0 \times x + 1 \times y - 2 = 0 \Rightarrow 0 \times 1 + y - 2 = 0 \Rightarrow y - 2 = 0\]
\[ \Rightarrow {\text{ For }}x = 2;{\text{ }}0 \times x + 1 \times y - 2 = 0 \Rightarrow 0 \times 2 + y - 2 = 0 \Rightarrow y - 2 = 0\]
\[ \Rightarrow {\text{ For }}x = 3;{\text{ }}0 \times x + 1 \times y - 2 = 0 \Rightarrow 0 \times 3 + y - 2 = 0 \Rightarrow y - 2 = 0\]
So x-coordinate can attain any real value without affecting the original equation, hence we can say the x-coordinate satisfies the complete x-axis.
Thus, this equation will represent a straight line which only has a y-coordinate as $2$ and x-coordinate can take any value, i.e. parallel to the x-axis and perpendicular to the y-axis.
It can be shown by the following diagram:

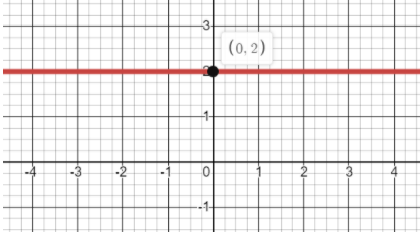
The red line in the graph represents the equation of the line $y = 2$ . It passes through the point $\left( {0,2} \right)$ on the y-axis.

Note:
In this question, the use of the general equation was a crucial part. An alternative approach can be to take random points from the line $y = 2$ and plot them on the graph. Find three of such points that lie on this line and plot them to graph the required line. Also, we know that equation of the form $y = a$ is parallel to the x-axis.