Question

How do you graph $f\left( x \right)=6x-4?$

Answer 1

Hint: We will find two or three points through which the graph of the given function passes. For that, we need to substitute some values for $x.$ This will give us the corresponding values of $y.$

Complete step by step solution:
Let us consider the given function for which we need to plot a graph, $f\left( x \right)=6x-4.$
For plotting the graph, we need two or three points through which the graph passes.
So, our primary task is to find the points through which the graph passes.
We will give values to $x.$ And when we apply these values in the given function, we will obtain the corresponding function values which are the $y-$coordinates.
To find the points, we will apply some random values to $x$ as the $x-$coordinates.
Let us take two numbers, $0$ and $1,$ to substitute for $x$ in the given function to obtain the corresponding function values.
Let us first apply $0$ to $x$ in the equation. We will get $f\left( 0 \right)=6x-4=0-4=-4.$
Since the function value corresponding to the $x-$coordinate $x=0,$ the corresponding $y-$coordinate is $y=-4.$
When we apply $x=1$ in the function, the function will become $f\left( 1 \right)=6\times 1-4=6-4=2.$
So, for the $x-$coordinate $x=1,$ the corresponding $y-$coordinate is $y=2.$
Therefore, the points $\left( 0,-4 \right)$ and $\left( 1,2 \right)$ are two points through which the graph of the given function passes.
Now, we have obtained two points as required.
So, the next task we need to do is to mark these points in the plane.
Then we will draw a line joining these points and then extend it to infinity in both positive and negative directions.

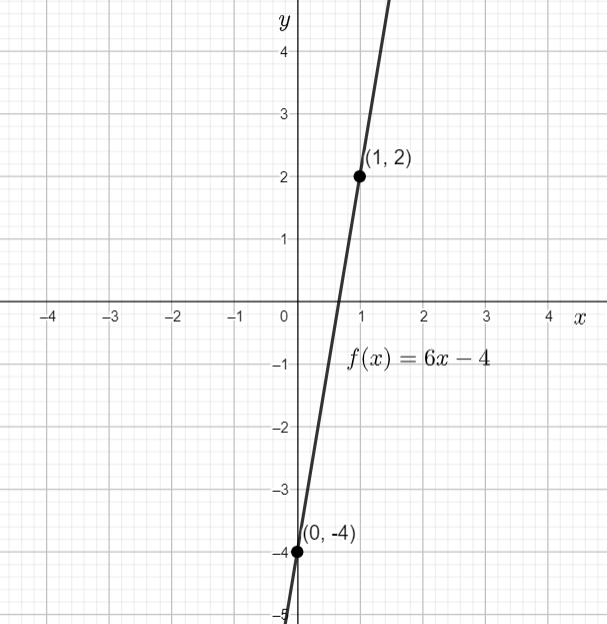
Hence the above graph is the graph for the given function $f\left( x \right)=6x-4.$

Note: We can determine if a function is one-one and onto when its graph is given. A function is one-one if every horizontal line touches the graph at most at one point. And a function is onto if every horizontal line intersects the graph at least once.