
How do you graph \[f\left( x \right)=2+\ln x\]?
Answer
528.6k+ views
Hint: This question is from the topic of exponential and logistic graphs which belongs to the chapter pre-calculus. In this question, we will draw the graph of \[f\left( x \right)=2+\ln x\]. In solving this question, we will first find the values of \[f\left( x \right)\] at x=0, 1, 2, 3, and \[\infty \]. After using these points and values of \[f\left( x \right)\] at those points, we will draw the graph of the given equation.
Complete step by step solution:
Let us solve this question.
In this question, we have asked to find the graph of the equation which is given in the question. The given equation is \[f\left( x \right)=2+\ln x\].
Let us first find out the value of \[f\left( x \right)\] at x=0. We can write
\[f\left( 0 \right)=2+\ln \left( 0 \right)\]
As we know that the value of \[\ln \left( 0 \right)\] is \[-\infty \], so we can write
\[\Rightarrow f\left( 0 \right)=2-\infty =-\infty \]
Now, let us first find out the value of \[f\left( x \right)\] at x=1. We can write
\[f\left( 1 \right)=2+\ln \left( 1 \right)\]
As we know that the value of \[\ln \left( 1 \right)\] is 0, so we can write
\[\Rightarrow f\left( 1 \right)=2+0=2\]
Now, let us find out the value of \[f\left( x \right)\] at x=2. We can write
\[f\left( 2 \right)=2+\ln \left( 2 \right)\]
As we know that the value of \[\ln \left( 2 \right)\] is 0.693, so we can write
\[\Rightarrow f\left( 2 \right)=2+0.693=2.693\]
Now, let us find out the value of \[f\left( x \right)\] at x=3.
\[f\left( 3 \right)=2+\ln \left( 3 \right)\]
Putting the value of \[\ln \left( 3 \right)\] as 1.0986, we can write
\[\Rightarrow f\left( 3 \right)=2+1.0986=3.0986\]
Now, let us find the value of \[f\left( x \right)\] at \[x=\infty \].
\[f\left( \infty \right)=2+\ln \left( \infty \right)\]
Putting the value of \[\ln \left( \infty \right)\] as \[\infty \] in the above equation, we can write
\[\Rightarrow f\left( \infty \right)=2+\infty =\infty \]
Now, we have got the following values:
Now, we will use the above table and draw the graph of \[f\left( x \right)=2+\ln x\]
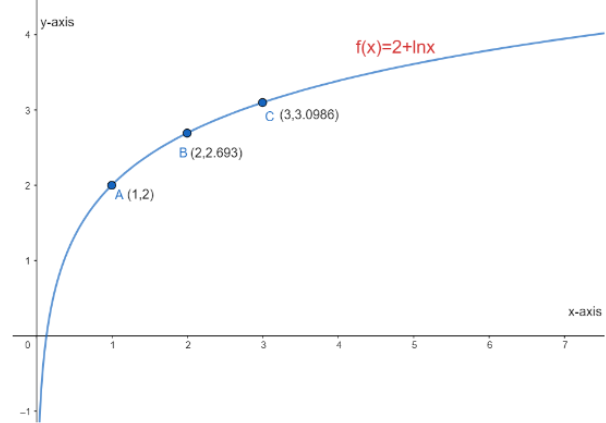
Now, we can see that at x=0, the value of f(x) is tending to negative or infinity at x equals to infinity, the value of f(x) is tending to infinity.
Note: We should have a better knowledge in the topic of exponential and logistic graphs to solve this type of question easily. We should remember the following values to solve this type of question easily:
Value of ‘e’ (that is exponential) = 2.71
\[\ln 0=-\infty \]
\[\ln 1=0\]
\[\ln 2=0.693\]
\[\ln 3=1.0986\]
\[\ln \infty =\infty \]
And, also remember that if \[\ln x=y\], then \[x={{e}^{y}}\]
Complete step by step solution:
Let us solve this question.
In this question, we have asked to find the graph of the equation which is given in the question. The given equation is \[f\left( x \right)=2+\ln x\].
Let us first find out the value of \[f\left( x \right)\] at x=0. We can write
\[f\left( 0 \right)=2+\ln \left( 0 \right)\]
As we know that the value of \[\ln \left( 0 \right)\] is \[-\infty \], so we can write
\[\Rightarrow f\left( 0 \right)=2-\infty =-\infty \]
Now, let us first find out the value of \[f\left( x \right)\] at x=1. We can write
\[f\left( 1 \right)=2+\ln \left( 1 \right)\]
As we know that the value of \[\ln \left( 1 \right)\] is 0, so we can write
\[\Rightarrow f\left( 1 \right)=2+0=2\]
Now, let us find out the value of \[f\left( x \right)\] at x=2. We can write
\[f\left( 2 \right)=2+\ln \left( 2 \right)\]
As we know that the value of \[\ln \left( 2 \right)\] is 0.693, so we can write
\[\Rightarrow f\left( 2 \right)=2+0.693=2.693\]
Now, let us find out the value of \[f\left( x \right)\] at x=3.
\[f\left( 3 \right)=2+\ln \left( 3 \right)\]
Putting the value of \[\ln \left( 3 \right)\] as 1.0986, we can write
\[\Rightarrow f\left( 3 \right)=2+1.0986=3.0986\]
Now, let us find the value of \[f\left( x \right)\] at \[x=\infty \].
\[f\left( \infty \right)=2+\ln \left( \infty \right)\]
Putting the value of \[\ln \left( \infty \right)\] as \[\infty \] in the above equation, we can write
\[\Rightarrow f\left( \infty \right)=2+\infty =\infty \]
Now, we have got the following values:
| \[x\] | 0 | 1 | 2 | 3 | \[\infty \] |
| \[f\left( x \right)\] | \[-\infty \] | 2 | 2.693 | 3.0986 | \[\infty \] |
Now, we will use the above table and draw the graph of \[f\left( x \right)=2+\ln x\]

Now, we can see that at x=0, the value of f(x) is tending to negative or infinity at x equals to infinity, the value of f(x) is tending to infinity.
Note: We should have a better knowledge in the topic of exponential and logistic graphs to solve this type of question easily. We should remember the following values to solve this type of question easily:
Value of ‘e’ (that is exponential) = 2.71
\[\ln 0=-\infty \]
\[\ln 1=0\]
\[\ln 2=0.693\]
\[\ln 3=1.0986\]
\[\ln \infty =\infty \]
And, also remember that if \[\ln x=y\], then \[x={{e}^{y}}\]
Recently Updated Pages
Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 7 Maths: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Maths: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




