Question

How do you graph $-4x+y > -6$?

Answer 1

Hint: We start solving the problem by finding the point on y-axis for which the equality (assumed) holds for the given equation by using the fact that the value of x-coordinate on the y-axis is zero. We then find the point on the x-axis for which the equality (assumed) holds for by using the fact that the value of y-coordinate on the x-axis is zero. We then represent these two points on the plot and then join those points to get the required plot and then map the area at which the condition holds true.

Complete step by step answer:
According to the problem, we are asked to plot the given inequality $-4x+y > -6$.
So, let us find the points on x-axis and y-axis which $-4x+y=-6$ holds true.
Now, let us find the point on the y-axis for which the equality holds true for $-4x+y=-6$. We know that the value of x-coordinate on the y-axis is zero. Let us substitute $x=0$ in the given equation to find the intersection point.
So, we get $-4\left( 0 \right)+y=-6$.
$\Rightarrow 0+y=-6$.
$\Rightarrow y=-6$.
So, the point that lies on the y-axis when equality holds true for $-4x+y=-6$ is $A\left( 0,-6 \right)$.
Now, let us find the point on x-axis for which the equality holds true for $-4x+y=-6$. We know that the value of y-coordinate on the x-axis is zero. Let us substitute $y=0$ in the given equation to find the intersection point.
So, we get $-4x+0=-6$.
$\Rightarrow -4x=-6$.
$\Rightarrow 4x=6$.
$\Rightarrow x=\dfrac{6}{4}$.
$\Rightarrow x=\dfrac{3}{2}$.
So, the point that lies on the x-axis when equality holds for $-4x+y=-6$ is $B\left( \dfrac{3}{2},0 \right)$.
Now, let us plot the given line by representing and joining the obtained two points and then mapping the area at which the given equation holds true on the graph by showing the points which holds true for equality with dotted lines which is as shown below:

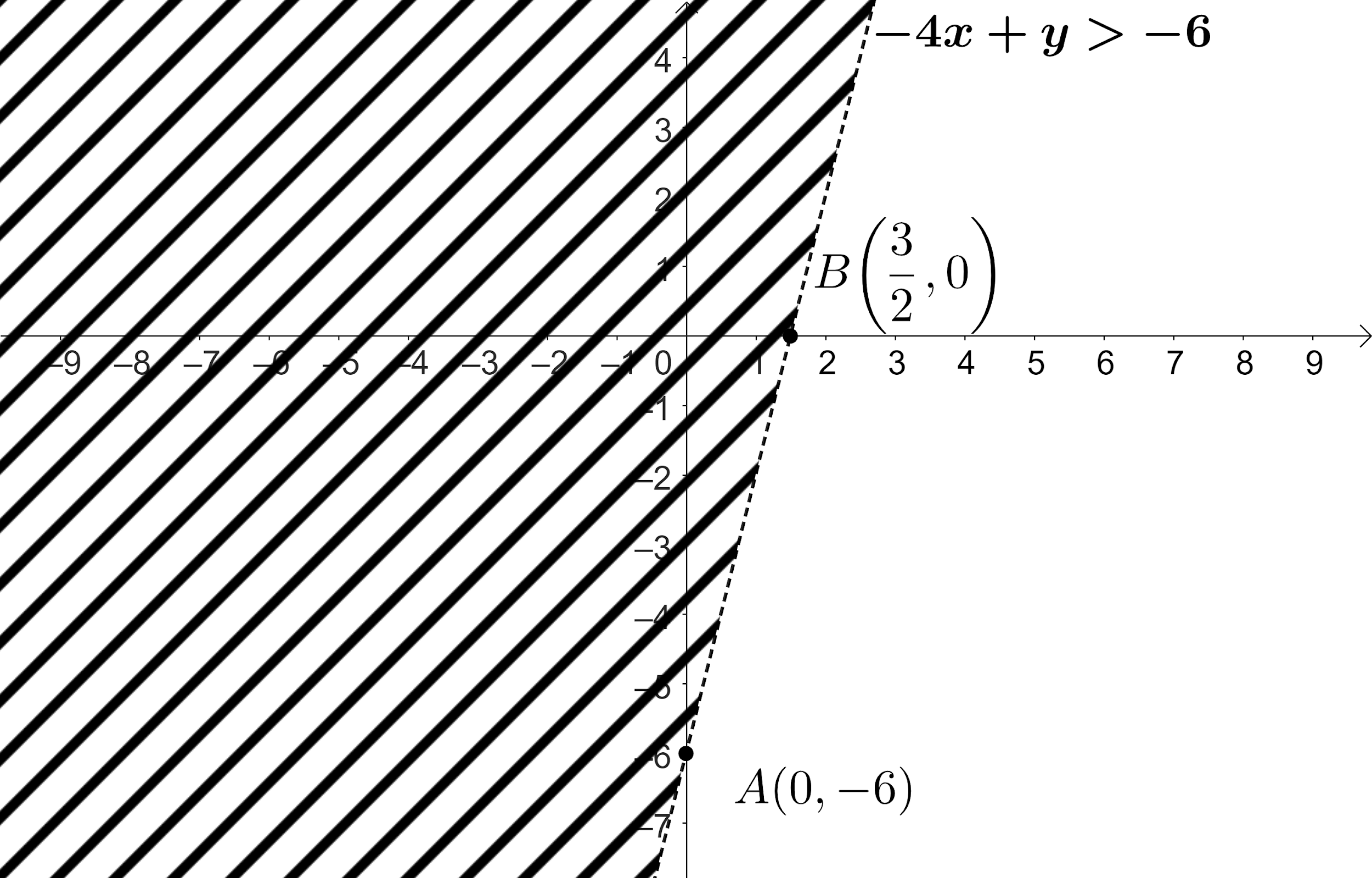
Note:
Here we have assumed equality as we know that there are infinite real numbers present between any two integers which will be difficult to plot each point by checking manually. Whenever we get this type of problem, we first try to find the points at which the given curve intersects both the axes by assuming equality. We should not forget to mark the equality line as dashed one as it is not included in the solution. Similarly, we can expect problems to plot the inequality $4x+3y < -12$ on the graph.