
How do you factor ${{x}^{3}}-4{{x}^{2}}-11x+30$ ?
Answer
544.5k+ views
Hint: For this expression, we put different values, generally whole numbers one by one of $x$ by hit and trial method in the expression and check which value of $x$ makes the expression equal to zero. We can then say that that value is the root and the corresponding $x-\left( value \right)$ will be the factor. Dividing the expression by this factor gives another expression, which can also be factorised in this way.
Complete step by step solution:The given expression is,
${{x}^{3}}-4{{x}^{2}}-11x+30$
We now put some whole numbers one by one in the above expression and see if the expression evaluates to zero or not. If the expression evaluates to zero, then that value of $x$ is the root of the expression and if it does not evaluate to zero, then it Is not a root. Let us put $x=0$ first. Doing so, the expression becomes,
$\begin{align}
& \Rightarrow {{0}^{3}}-4{{\left( 0 \right)}^{2}}-11\left( 0 \right)+30 \\
& \Rightarrow 30 \\
\end{align}$
Thus, $x=0$ does not satisfy the expression. So, we now put $x=1$ . Doing so, the expression becomes,
$\begin{align}
& \Rightarrow {{1}^{3}}-4{{\left( 1 \right)}^{2}}-11\left( 1 \right)+30 \\
& \Rightarrow 16 \\
\end{align}$
Thus, $x=1$ does not satisfy the expression. So, we now put $x=2$ . Doing so, the expression becomes,
$\begin{align}
& \Rightarrow {{2}^{3}}-4{{\left( 2 \right)}^{2}}-11\left( 2 \right)+30 \\
& \Rightarrow 0 \\
\end{align}$
This means that $x=2$ is a root of the expression or that $x-2$ is a factor of it. We now divide ${{x}^{3}}-4{{x}^{2}}-11x+30$ by $x-2$ . We get ${{x}^{2}}-2x-15$ as quotient. This means,
${{x}^{3}}-4{{x}^{2}}-11x+30=\left( x-2 \right)\left( {{x}^{2}}-2x-15 \right)$
We now factorise ${{x}^{2}}-2x-15$ . If we put $x=-3$ in this expression, we get,
$\Rightarrow {{\left( -3 \right)}^{2}}-2\left( -3 \right)-15=0$
This means that $x=-3$ is a root of the expression ${{x}^{2}}-3x-10$ or that $x+3$ is a factor of ${{x}^{2}}-2x-15$ . Dividing ${{x}^{2}}-2x-15$ by $x+3$ , we get, $x-5$ as a quotient . Thus, ${{x}^{2}}-2x-15$ can be written as,
$\Rightarrow {{x}^{2}}-2x-15=\left( x+3 \right)\left( x-5 \right)$
Thus, summing up every expression we get, we can write that,
$\Rightarrow {{x}^{3}}-4{{x}^{2}}-11x+30=\left( x-2 \right)\left( x+3 \right)\left( x-5 \right)$
Therefore we can conclude that the given expression can be factorised as $\left( x-2 \right)\left( x+3 \right)\left( x-5 \right)$ .
Note: We can see that the given expression is quite big. So, solving it by using conventional means of factorisation may prove time taking and at the end, we may even be not able to factorise it. So, this method is the best for these problems. But, sometimes the vanishing factor method may also take time. For those situations, we use the graphical approach. We plot the respective graph of the expression and see where it cuts the $x-axis$ . Those values will be the roots and $x$ minus those values will be the factors.
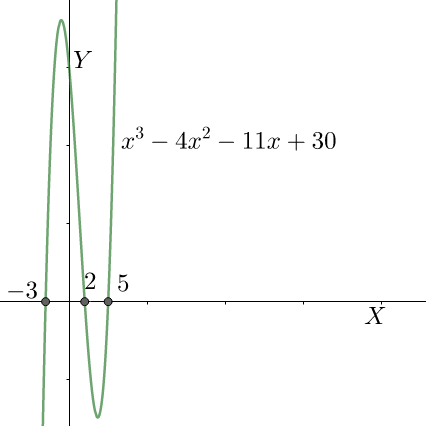
Complete step by step solution:The given expression is,
${{x}^{3}}-4{{x}^{2}}-11x+30$
We now put some whole numbers one by one in the above expression and see if the expression evaluates to zero or not. If the expression evaluates to zero, then that value of $x$ is the root of the expression and if it does not evaluate to zero, then it Is not a root. Let us put $x=0$ first. Doing so, the expression becomes,
$\begin{align}
& \Rightarrow {{0}^{3}}-4{{\left( 0 \right)}^{2}}-11\left( 0 \right)+30 \\
& \Rightarrow 30 \\
\end{align}$
Thus, $x=0$ does not satisfy the expression. So, we now put $x=1$ . Doing so, the expression becomes,
$\begin{align}
& \Rightarrow {{1}^{3}}-4{{\left( 1 \right)}^{2}}-11\left( 1 \right)+30 \\
& \Rightarrow 16 \\
\end{align}$
Thus, $x=1$ does not satisfy the expression. So, we now put $x=2$ . Doing so, the expression becomes,
$\begin{align}
& \Rightarrow {{2}^{3}}-4{{\left( 2 \right)}^{2}}-11\left( 2 \right)+30 \\
& \Rightarrow 0 \\
\end{align}$
This means that $x=2$ is a root of the expression or that $x-2$ is a factor of it. We now divide ${{x}^{3}}-4{{x}^{2}}-11x+30$ by $x-2$ . We get ${{x}^{2}}-2x-15$ as quotient. This means,
${{x}^{3}}-4{{x}^{2}}-11x+30=\left( x-2 \right)\left( {{x}^{2}}-2x-15 \right)$
We now factorise ${{x}^{2}}-2x-15$ . If we put $x=-3$ in this expression, we get,
$\Rightarrow {{\left( -3 \right)}^{2}}-2\left( -3 \right)-15=0$
This means that $x=-3$ is a root of the expression ${{x}^{2}}-3x-10$ or that $x+3$ is a factor of ${{x}^{2}}-2x-15$ . Dividing ${{x}^{2}}-2x-15$ by $x+3$ , we get, $x-5$ as a quotient . Thus, ${{x}^{2}}-2x-15$ can be written as,
$\Rightarrow {{x}^{2}}-2x-15=\left( x+3 \right)\left( x-5 \right)$
Thus, summing up every expression we get, we can write that,
$\Rightarrow {{x}^{3}}-4{{x}^{2}}-11x+30=\left( x-2 \right)\left( x+3 \right)\left( x-5 \right)$
Therefore we can conclude that the given expression can be factorised as $\left( x-2 \right)\left( x+3 \right)\left( x-5 \right)$ .
Note: We can see that the given expression is quite big. So, solving it by using conventional means of factorisation may prove time taking and at the end, we may even be not able to factorise it. So, this method is the best for these problems. But, sometimes the vanishing factor method may also take time. For those situations, we use the graphical approach. We plot the respective graph of the expression and see where it cuts the $x-axis$ . Those values will be the roots and $x$ minus those values will be the factors.

Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




