Question

How do you draw slope lines?

Answer 1

Hint:Slope lines are the solutions of the first order differential equation of any equation.

Complete step by step solution:
A differentiable function - and the answers for differential equations should be differentiable- - has tangent lines at each point. We should draw little bits of a portion of these tangent lines of the function.

A tool that is used to graphically obtain the solutions of the first order differential equation of any equation are known as slope fields. The slant, ${y^`}(x)$, of the solutions $y(x)$, is resolved once we know the values for x and y , e.g., on the off chance that $x = 1$ and $y = - 1$, at that point the slant of the solution y(x) going through the point (1,- 1) will be $( - 2) \times 1 \times ( - 1) = 2$. In the event that we graph y(x) in the x-y plane, it will have slant 2, given $x = 1$ and $y = - 1$. We demonstrate this graphically by embeddings a little line fragment at the point (1,- 1) of incline 2.

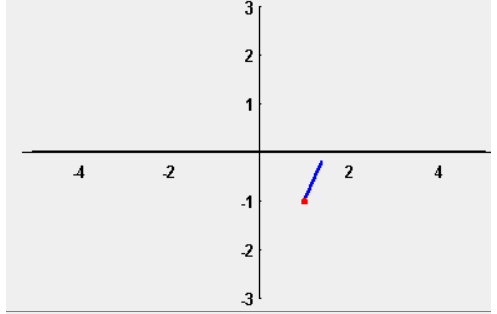
Consequently, the arrangement of the differential condition with the underlying condition $y(1) = -1$will appear to be like this line section as long as we remain near $x = 1$
Obviously, doing this at only one point doesn't give a lot of data about the arrangements. We need to do this at the same time at numerous focuses in the x-y plane.

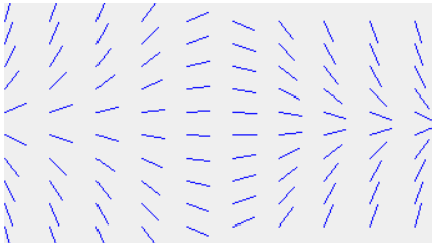
Note: 1. Cartesian Plane: A Cartesian Plane is given its name by the French mathematician Rene Descartes, who first used this plane in the field of mathematics .It is defined as the two mutually perpendicular number line , the one which is horizontal is given name x-axis and the one which is vertical is known as a y-axis. With the help of these axes we can plot any point on this cartesian plane with the help of an ordered pair of numbers.