Question

How do you calculate $ \cos (\dfrac{{3\pi }}{2}) $ ?

Answer 1

Hint: This problem can be solved using two methods.
 $ \bullet $ Using $ \cos 3x $ formula.
 $ \bullet $ Using Unit circle.
In the first method, first we are going to convert the angle from radian to degree and then suppose the converted degree as 3x to find the value of x. After finding the value of x, we can use the formula for $ \cos 3x $ .

Complete step by step solution:
Method 1: Using $ \cos 3x $ formula
In this method, we are going to use a direct formula to solve the question.
Here, we are supposed to calculate the value of $ \cos (\dfrac{{3\pi }}{2}) - - - - - \left( 1 \right) $ .
Now, to use the formula, we need to set some things as per the formula.
First of all the given expression is in radian and we need to convert that into degrees.
So, we know that, $ \pi = 180^\circ $
Substitute $ \pi $ by 180 in equation (1)
 $
   \Rightarrow \cos \left( {\dfrac{{3\pi }}{2}} \right) = \cos \left( {\dfrac{{3 \times 180}}{2}} \right) \\
   \Rightarrow \cos \left( {\dfrac{{3\pi }}{2}} \right) = \cos 270^\circ - - - - - \left( 2 \right) \;
  $
To use the formula of $ \cos 3x $ , we need to find the value of x.
For that, let
 $
   \Rightarrow 3x = 270 \\
   \Rightarrow x = 90 \;
  $
Now, equation (2) can be written as
 $ \Rightarrow \cos \left( {\dfrac{{3\pi }}{2}} \right) = \cos \left( {3 \times 90^\circ } \right) - - - - \left( 3 \right) $
Now, for solving $ \cos \left( {3 \times 90} \right) $ compare equation (3) with
 $ \cos 3x = 4{\cos ^3}x - 3\cos x $ - - - - - - -(4)
Comparing these two equations, we get $ x = 90^\circ $
Therefore, putting value of x in equation (4), we get
 $ \Rightarrow \cos \left( {3 \times 90} \right) = 4{\cos ^3}90 - 3\cos 90 - - - - \left( 5 \right) $
Now, we know that $ \cos 90 = $ 0
Therefore, equation (5) becomes
 $
   \Rightarrow \cos \left( {3 \times 90} \right) = 4{\left( 0 \right)^3} - 3\left( 0 \right) \\
   \Rightarrow \cos 270 = 0 - 0 \\
   \Rightarrow \cos 270 = 0 \;
  $
which is nothing but $ \cos (\dfrac{{3\pi }}{2}) $ .
 $ \Rightarrow \cos \left( {\dfrac{{3\pi }}{2}} \right) = \cos 270 = 0 $
So, the correct answer is “0”.

Note: Method 2: Using Unit Circle.
In this method, we are going to draw a unit circle first of all.

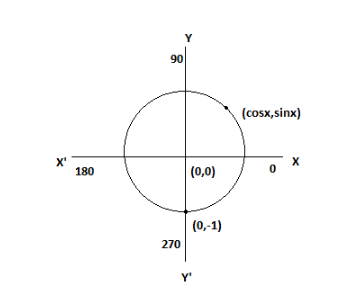
Now, each and every point on this unit circle is represented as $ \left( {\cos \theta ,\sin \theta } \right) - - - - \left( 1 \right) $ .
We need to find $ \cos \left( {\dfrac{{3\pi }}{2}} \right) $ .
 $ \dfrac{{3\pi }}{2} $ Lies on negative Y-Axis.
As our point is on the negative Y-Axis, the x coordinate will be zero and the y coordinate will be $ - 1 $ as the distance of every point from origin on the unit circle is always 1.
Comparing with equation (1)
 $ \left( {\cos \theta ,\sin \theta } \right) = \left( {0, - 1} \right) $
Therefore, $ \cos \left( {\dfrac{{3\pi }}{2}} \right) = 0 $