Question

How do I graph $y = {x^2} - 6x + 5$.

Answer 1

Hint: The given problem deals with the plotting of the graph of the quadratic equation. We will find the different points, which are passing through the given quadratic equation. We will substitute the different values of $x$ in the quadratic equation and find the respective value of the $y$. First we will substitute $x = 0$ and find the value of $y$. Again we will substitute $y = 0$ in the given quadratic equation and find the corresponding value of $x$. Again we will substitute $x = 1$ in the given quadratic equation and find the value of $y$. In the same manner we will substitute the different values of $x = - 1,2, - 2,3, - 3$ and find the corresponding value of $y$. These points will lie on the given quadratic equation and they will satisfy the given equation.

Complete step by step solution:
Step: 1 the given quadratic equation is,
$y = {x^2} - 6x + 5$
So substitute $x = 0$ in the given quadratic equation and find the value of $y$.
$
   \Rightarrow y = {x^2} - 6x + 5 \\
   \Rightarrow y = 0 - 0 + 5 \\
   \Rightarrow y = 5 \\
 $
So the point $\left( {0,5} \right)$ lies on the curve of the quadratic equation.
 Step: 2 now substitute $y = 0$ in the given equation and find the value of $x$.
$
   \Rightarrow y = {x^2} - 6x + 5 \\
   \Rightarrow 0 = {x^2} - 6x + 5 \\
 $
Solve the equation to find the value of $x$.
The equation is a quadratic equation, so we will first multiply the constant term of the equation with coefficient of the ${x^2}$ and then we will find the factor, which in addition or subtraction, gives the middle term of the quadratic equation.
$
   \Rightarrow {x^2} - 6x + 5 = 0 \\
   \Rightarrow {x^2} - 5x - x + 5 = 0 \\
   \Rightarrow x\left( {x - 5} \right) - 1\left( {x - 5} \right) = 0 \\
   \Rightarrow \left( {x - 1} \right)\left( {x - 5} \right) = 0 \\
 $
Equate the factors equal to zero.
$
   \Rightarrow x - 1 = 0 \\
   \Rightarrow x = 1 \\
 $
Consider the second factor.
$
   \Rightarrow x - 5 = 0 \\
   \Rightarrow x = 5 \\
 $
Therefore the point $\left( {1,0} \right)$ and $\left( {5,0} \right)$ passes through the given equation.
Now substitute $x = - 1$ in the equation and find the value of $y$.
$
   \Rightarrow y = {x^2} - 6x + 5 \\
   \Rightarrow y = 1 + 6 + 5 \\
   \Rightarrow y = 12 \\
 $
Therefore the points $\left( { - 1,12} \right),\left( {1,0} \right)\left( {0,5} \right)\left( {5,0} \right)$ will lie on the curve of given quadratic equation.
Step: 3 plot these given points on the graph and connect them.

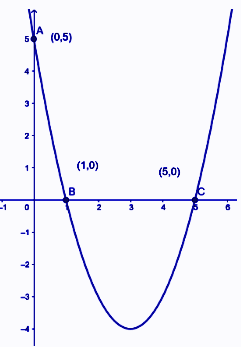
Therefore, we can draw the graph of a given quadratic equation.

Note:
Students are advised to not join the corresponding points, which lies on the given quadratic equation by simply straight lines. First they must substitute $x = 0,1, - 1,$ and find the corresponding value of $y$ . They must avoid mistakes while calculating the points.