Question

How are vector diagrams used?

Answer 1

Hint: Vector diagrams are diagrams that use a vector arrow to represent the direction and relative magnitude of a vector quantity. To describe the velocity of a moving object during its motion, vector diagrams can be used. For instance, to represent the motion of a car moving down the road, a vector diagram could be used.

Complete solution:

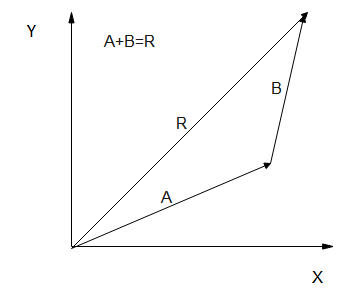
1.The magnitude of a vector quantity is represented by the size of the vector arrow in a vector diagram. If the arrow size is the same in each consecutive frame of the vector diagram, then the vector magnitude is constant.
2.The diagrams below illustrate a car's speed during its motion. The size of the velocity vector is constant in the top diagram, so the diagram depicts a motion of constant velocity.
3.The size of the velocity vector is increasing in the bottom diagram, so the diagram depicts a motion with increasing velocity, i.e. an acceleration.
4.By a process called vector resolution, vectors can be resolved into two or more smaller components. In vector space, any vector can be resolved into two components, namely the horizontal and vertical components.
5.The horizontal component is a product of the vector's magnitude and the horizontal angle cosine. The vertical component of a vector is the product of the vector's magnitude and the horizontal angle of the sinus.

Note:
To represent any vector quantity, vector diagrams can be used. Vector diagrams will be used in future studies to represent a range of physical quantities, such as acceleration, force, and momentum. To represent the direction and relative size of a quantity, be familiar with the concept of using a vector arrow. As we go further in our studies of the physics of motion, it will become a very significant representation of the motion of an object.