Question

Where will the hour hand of a clock stop if it starts from 10 and turns through 3 right angles ?

Answer 1

Hint: In this particular type of question first we need to convert 1 hour on a clock into degrees of a circle. Then we need to convert the given information into degrees and add it to the angle which the clock makes at 10 to find the required answer.

Complete Step-by-Step solution:

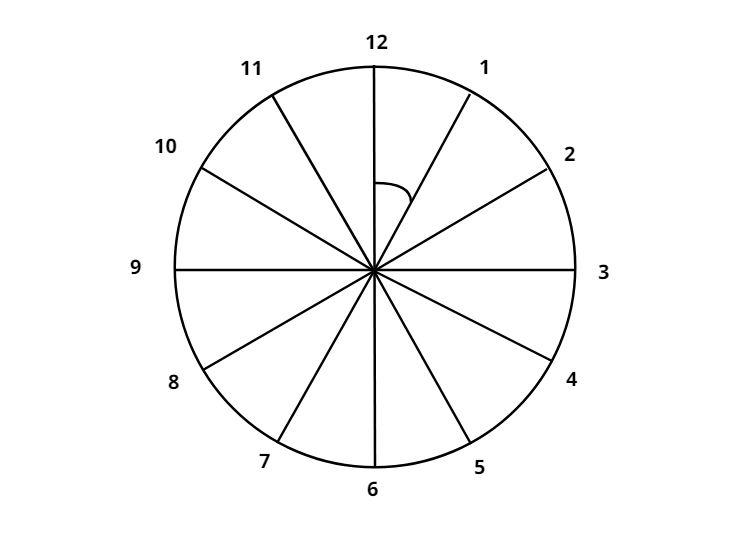
We know that the clock is divided into 12 parts or 12 hours .
$ \Rightarrow 360^\circ {\text{ is divided into 12 parts of 1 hour each}}$
Hence angle swept by hour hand in 1 hour = $\dfrac{{360}}{{12}} = 30^\circ $
Let the anti clockwise side of 12 O clock represents negative angles and the clockwise side behaves as a positive angle .
Therefore 10 at the clock would be $\left( {12 - 10} \right) \times 30^\circ = 60^\circ $
But 10 is in the anti clockwise direction therefore it is represented by $ - 60^\circ $ and the hour hand lies on it.
Now if the hour hand swipes 3 right angles i.e. $3 \times 90 = 270^\circ $ clockwise , then the angle at which we reach will be equal to $ - 60^\circ + 270^\circ = 210^\circ $ on the clockwise direction .
Which is $\dfrac{{210}}{{30}} = 7$ o'clock in the clock.
Hence the hour hand will stop at 7 on the clock.

Note: Remember to draw a circle and divide it in 12 parts to find all the angles the hour hand is making at different times of the day. These types of questions require good imagination and proper understanding of the basics behind working of a clock.