
Hiep is writing a coordinate proof to show that the midsegment of a trapezoid is parallel to its bases. He starts by assigning coordinates as given, where RS is the midsegment of trapezoid KLMN. am I correct?
Answer
522.9k+ views
Hint: To solve this question, we first calculate the midpoints for the given sides KN and LM which are R and S. We calculate this by using the midpoint formula. Then, we find the slope of this line RS. Similarly, we find the slope of the lines KN and LM and check if this line RS is parallel to KN and LM or not.
Complete step by step solution:
Let us consider the below figure of a trapezium with the points and their coordinates represented by,
Coordinates of point K: $\left( 0,0 \right)$
Coordinates of point L: $\left( a,0 \right)$
Coordinates of point M: $\left( b,c \right)$
Coordinates of point N: $\left( d,c \right)$
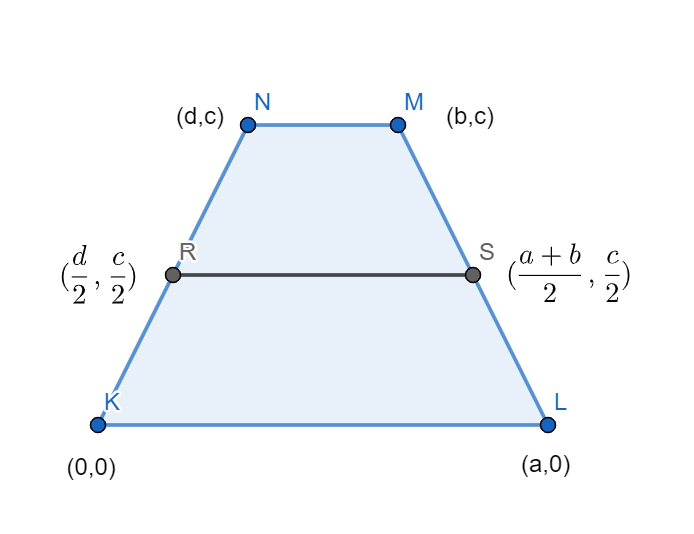
We now use the midpoint formula to calculate the mid points R and S. The midpoint formula is given by $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right).$ Here, the end points of the line segment are given by the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right).$
The point R is the midpoint of the line segment KN. Therefore,
$\Rightarrow \text{Coordinates of R = }\left( \dfrac{d+0}{2},\dfrac{c+0}{2} \right)$
Simplifying this,
$\Rightarrow \text{Coordinates of R = }\left( \dfrac{d}{2},\dfrac{c}{2} \right)$
Similarly, S is the midpoint of the line segment LM. Therefore,
$\Rightarrow \text{Coordinates of S = }\left( \dfrac{a+b}{2},\dfrac{c+0}{2} \right)$
Simplifying this,
$\Rightarrow \text{Coordinates of S = }\left( \dfrac{a+b}{2},\dfrac{c}{2} \right)$
Now we are required to find the slope of the given line segment RS. The slope for a line with two endpoints given by $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by,
$\Rightarrow \text{Slope = }\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Hence, the slope for the line RS with endpoints given by $\left( \dfrac{d}{2},\dfrac{c}{2} \right)$ and $\left( \dfrac{a+b}{2},\dfrac{c}{2} \right)$ is
$\Rightarrow \text{Slope of RS = }\dfrac{\dfrac{c}{2}-\dfrac{c}{2}}{\dfrac{a+b}{2}-\dfrac{d}{2}}$
Since the numerator term is 0, the slope of RS is 0,
$\Rightarrow \text{Slope of RS = }0$
Similarly, we find the slope of the lines KL and NM using the same slope formula,
Slope for the line KL with endpoints given by $\left( 0,0 \right)$ and $\left( a,0 \right)$ is
$\Rightarrow \text{Slope of KL = }\dfrac{0-0}{a-0}$
Since the numerator term is 0, the slope of KL is 0,
$\Rightarrow \text{Slope of KL = }0$
Slope for the line NM with endpoints given by $\left( d,c \right)$ and $\left( b,c \right)$ is
$\Rightarrow \text{Slope of NM = }\dfrac{c-c}{b-d}$
Since the numerator term is 0, the slope of NM is 0,
$\Rightarrow \text{Slope of NM = }0$
Since all the slopes are the same which is equal to 0 for the given coordinates, the midsegment RS of the trapezoid is parallel to its top base NM and lower base KL.
Hence, it is proved that the midsegment RS of the trapezoid is parallel to its top base NM and lower base KL which is correct.
Note: It is essential to know the midpoint and slope calculation formulae for a given set of points. Basic knowledge of geometry is required to identify the kind of figure in the given question. Also, it is important to note that if the y-coordinates of two points are equal, they result in a 0 slope which means that the line is parallel to the x-axis in the coordinate plane.
Complete step by step solution:
Let us consider the below figure of a trapezium with the points and their coordinates represented by,
Coordinates of point K: $\left( 0,0 \right)$
Coordinates of point L: $\left( a,0 \right)$
Coordinates of point M: $\left( b,c \right)$
Coordinates of point N: $\left( d,c \right)$

We now use the midpoint formula to calculate the mid points R and S. The midpoint formula is given by $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right).$ Here, the end points of the line segment are given by the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right).$
The point R is the midpoint of the line segment KN. Therefore,
$\Rightarrow \text{Coordinates of R = }\left( \dfrac{d+0}{2},\dfrac{c+0}{2} \right)$
Simplifying this,
$\Rightarrow \text{Coordinates of R = }\left( \dfrac{d}{2},\dfrac{c}{2} \right)$
Similarly, S is the midpoint of the line segment LM. Therefore,
$\Rightarrow \text{Coordinates of S = }\left( \dfrac{a+b}{2},\dfrac{c+0}{2} \right)$
Simplifying this,
$\Rightarrow \text{Coordinates of S = }\left( \dfrac{a+b}{2},\dfrac{c}{2} \right)$
Now we are required to find the slope of the given line segment RS. The slope for a line with two endpoints given by $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by,
$\Rightarrow \text{Slope = }\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Hence, the slope for the line RS with endpoints given by $\left( \dfrac{d}{2},\dfrac{c}{2} \right)$ and $\left( \dfrac{a+b}{2},\dfrac{c}{2} \right)$ is
$\Rightarrow \text{Slope of RS = }\dfrac{\dfrac{c}{2}-\dfrac{c}{2}}{\dfrac{a+b}{2}-\dfrac{d}{2}}$
Since the numerator term is 0, the slope of RS is 0,
$\Rightarrow \text{Slope of RS = }0$
Similarly, we find the slope of the lines KL and NM using the same slope formula,
Slope for the line KL with endpoints given by $\left( 0,0 \right)$ and $\left( a,0 \right)$ is
$\Rightarrow \text{Slope of KL = }\dfrac{0-0}{a-0}$
Since the numerator term is 0, the slope of KL is 0,
$\Rightarrow \text{Slope of KL = }0$
Slope for the line NM with endpoints given by $\left( d,c \right)$ and $\left( b,c \right)$ is
$\Rightarrow \text{Slope of NM = }\dfrac{c-c}{b-d}$
Since the numerator term is 0, the slope of NM is 0,
$\Rightarrow \text{Slope of NM = }0$
Since all the slopes are the same which is equal to 0 for the given coordinates, the midsegment RS of the trapezoid is parallel to its top base NM and lower base KL.
Hence, it is proved that the midsegment RS of the trapezoid is parallel to its top base NM and lower base KL which is correct.
Note: It is essential to know the midpoint and slope calculation formulae for a given set of points. Basic knowledge of geometry is required to identify the kind of figure in the given question. Also, it is important to note that if the y-coordinates of two points are equal, they result in a 0 slope which means that the line is parallel to the x-axis in the coordinate plane.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




