Question

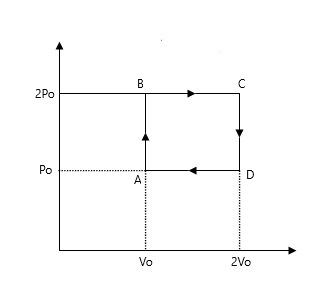
Helium gas goes through a cycle ABCDA (consisting of two isochoric and two isobaric lines) as shown in the figure. Calculate the approximate efficiency of the cycle. (Assume the gas to be close to ideal gas).

Answer 1

Hint: We have to calculate the efficiency and efficiency is the ratio of work done and heat given or taken
$\eta =\dfrac{W}{Q}$
Further, the heat in this process can find out with the help of Molar heat capacities. Molar heat capacity is the quantity of heat required to raise the temperature of 1 mole of a substance by 1 degree. Efficiency doesn’t have any units.

Complete Solution :
If we look at the process AB then there is an increase of pressure in it and the process BC, the volume is increasing, therefore the temperature is increasing.
Now, you may ask that how the temperature is increasing then, we all know if the volume is constant then pressure is directly proportional to the temperature in AB path and when pressure is constant in BC then the volume is directly proportional to the temperature.
The increase in temperature can be calculated by:
$Q=n{{\left( {{C}_{v}}\Delta T \right)}_{AB}}+n{{\left( {{C}_{p}}\Delta T \right)}_{BC}}$ ${{C}_{P}}=\dfrac{3}{2}R$
$\Rightarrow Q=\dfrac{3}{2}{{\left( nR\Delta T \right)}_{AB}}+\dfrac{5}{2}{{\left( nR\Delta T \right)}_{BC}}$ ${{C}_{V}}=\dfrac{5}{2}R$
$\Rightarrow Q=\dfrac{3}{2}\left( {{P}_{0}}{{V}_{0}} \right)+\dfrac{5}{2}\left( 2{{P}_{0}}{{V}_{0}} \right)$ $PV=nRT$ $\left( n = 2for{{C}_{P}} \right)$
$\therefore Q=\dfrac{13}{2}{{P}_{0}}{{V}_{0}}$

We have found the heat required in the process, now we will find the work done required for it.
W=Area under the P-V graph
$W=P\left( 2{{V}_{0}}-{{V}_{0}} \right)$
$\Rightarrow W={{P}_{0}}{{V}_{0}}$
Now, we have both the work and heat with us, let us put it in the formula of efficiency.
$\eta =\dfrac{W}{Q}$
Putting the values
$\eta =\dfrac{{{P}_{0}}{{V}_{0}}}{\dfrac{13}{2}{{P}_{0}}{{V}_{0}}}$
$\Rightarrow \eta =\dfrac{2}{13}=0.0154$
$\therefore \eta = 15.4%$
Therefore, the efficiency of the process is 15.4%

Note: The process which is occurring above in the CD and DA part is not considered. As in two of the processes, both the volume and temperature are decreasing and due to the negative sign later in the process, the value would have become zero.