Question

What is HCF of ${2^3} \times 5$ and ${2^2} \times {5^2}$.

Answer 1

Hint: To find the highest common factor of two numbers, we can use three methods. One is the prime factorization method, next is the division method and the last is the factorization method. In this example, we will use the prime factorization method. For finding HCF by the prime factorization method, we factorize the two numbers into prime numbers which are known as prime factors.

Complete step-by-step solution:
The two numbers given are: ${2^3} \times 5$ and ${2^2} \times {5^2}$ that is $40$ and $100$.
Now we will make the prime factor tree for better understanding,
The prime factor tree for the number $40$and $100$ is as follows:

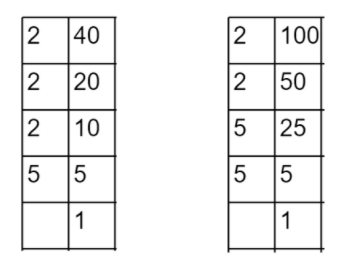
We can write number $40 = 2 \times 2 \times 2 \times 5$ and $100 = 2 \times 2 \times 5 \times 5$
The first common factor of $40$ and $100$ is $2$.
The second common factor of $40$ and $100$ is $2$.
The third common factor of $40$ and $100$ is $5$.
Therefore, the common factors of $40$ and $100$ are $2,2,5$ .
The highest common factor i.e., the highest common factor is the product of all the common factors between the two numbers.
Here the highest common factor for the numbers $40$ and $100$ or ${2^3} \times 5$ and ${2^2} \times {5^2}$ will be the product of the common factors $2,2,5$ .
HCF of ${2^3} \times 5$ and ${2^2} \times {5^2}$ = $2 \times 2 \times 5 = 20$.
Therefore, the highest common factor of ${2^3} \times 5$ and ${2^2} \times {5^2}$ = $20$ .

Note: The largest common factor of all the given numbers is known as HCF. The highest common factor is also known as Greatest Common Divisor as it divides two or more numbers without any remainder left. The easiest way to find the Highest common factor is by making a prime factor tree.