Question

Hari standing on the top of a building, sees the top of a tower at an angle of elevation of ${{50}^{\circ }}$ and the foot of the tower at an angle of depression of ${{20}^{\circ }}$. Height of Hari is 1.6 meter and the height of the building on which he is standing is 9.2 meter.
(a). Draw a rough sketch according to the given information.
(b). How far is the tower from the building?
(c). Calculate the height of the tower.
$\sin {{20}^{\circ }}=0.34,\cos {{20}^{\circ }}=0.94,\tan {{20}^{\circ }}=0.36,\sin {{50}^{\circ }}=0.77,\cos {{50}^{\circ }}=0.64\tan {{50}^{\circ }}=1.19$

Answer 1

Hint: Draw a suitable diagram representing building, tower and boy and their lengths with the angle of elevation and depression as well. Now use $\tan \theta =\dfrac{perpendicular}{base}$ in the triangles where the angle of elevation and depression are involved. Use the values given in the problem.

Complete step-by-step answer:

Here, first of all, we need to draw a suitable diagram with the given information in the question. We have been provided that
i. Angle of elevation of Hari on building to the top of the tower is ${{50}^{\circ }}$ and angle of depression of foot of the tower is ${{20}^{\circ }}$.
ii. Height of Hari = 1.6m, Height of building on which Hari is standing = 9.2m
Hence, diagram can be given as

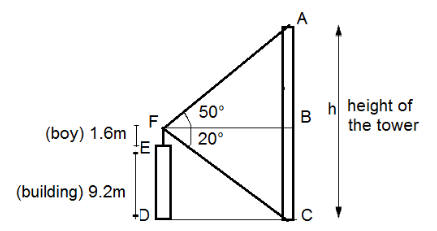
Now, we can observe that the length of BC can be given by adding EF and ED as BC = FD as CBFD is a rectangle by symmetry.
So, we get
BC = 1.6 + 9.2m
BC = 10.8m
Now, we can take $\tan {{50}^{\circ }}$ and $\tan {{20}^{\circ }}$ in the triangles ABF and FBC to get the length AB and hence the length AC(height of tower).
So, we know that
$\tan \theta =\dfrac{perpendicular}{base}$
Hence, taking $\tan {{50}^{\circ }}$in $\Delta ABF$ , we get
$\tan {{50}^{\circ }}=\dfrac{AB}{FB}$…………….. (i)
Similarly, we can take $\tan {{20}^{\circ }}$in $\Delta FBC$, we get
$\tan {{20}^{\circ }}=\dfrac{BC}{FB}$
We know BC = 10.8m, So, we get
$\tan {{20}^{\circ }}=\dfrac{10.8}{FB}$ ………………. (ii)
Now, coming to the question
Figure 1 is a rough sketch according to the given question.
Here, we have to calculate the distance between buildings and tower i.e. FB from the diagram. So, we can solve this part by using the equation (ii). So, we have
$\tan {{20}^{\circ }}=\dfrac{10.8}{FB}$
Value of $\tan {{20}^{\circ }}$ from the question is 0.36. so, we can put $\tan {{20}^{\circ }}=0.36$ in the above equation. So, we get
$\begin{align}
  & 0.36=\dfrac{10.8}{FB} \\
 & \Rightarrow FB=\dfrac{10.8}{0.36} \\
 & \Rightarrow FB=\dfrac{1080}{36}=30m \\
\end{align}$
Hence, the distance between tower and building is 30m.
Here, we need to determine the height of the tower which can be given from the diagram as
h = AB + BC …………………… (iii)
where BC = 10.8m
We can calculate the height of the tower using the equation (i). so, we get
$\tan {{50}^{\circ }}=\dfrac{AB}{FB}$
Now, we know the value of FB is 30m as we have calculated it in the previous part of the question. So, we get
$\tan {{50}^{\circ }}=\dfrac{AB}{30}$
 Now, put $\tan {{50}^{\circ }}=1.19$ from the question. So, we get
$\begin{align}
  & 1.19=\dfrac{AB}{30} \\
 & AB=30\times 1.19=3\times 11.9 \\
 & AB=35.7m \\
\end{align}$
Hence, we can put values of AB and BC in the question (iii) to get the height ‘h’ of the tower. So, we get
h = 35.7 + 10.8
h = 46.5m
This is the height of the tower.

Note: One may use $\tan $ and $\cot $ functions only for getting distance between tower and building and height of the tower as well. Using any other functions will be a waste of time as we do not require the sides AF and FC. So, be clear with the functions as well i.e. which function of trigonometry uses which sides of the triangle.
Use values of $\tan 50$ and $\tan {{20}^{\circ }}$. Other values are given for distracting you so that you may try to involve other functions as well.
Don’t ignore the length of the boy as well to get an accurate answer.