Question

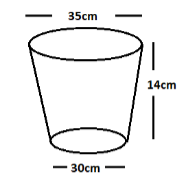
Hanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameter of it’s two circular faces as 30cm and 35cm and the vertical height of the mould is 14cm. If each $c{m^3}$ of the molasses has mass about 1.2gm, find the mass of the molasses that can be poured into each mould. Take $\left( {\pi = \dfrac{{22}}{7}}\right)$

Answer 1

Hint: According to given in the question we have to find the mass of the molasses that can be poured into each mould when Hanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameter of it’s two circular faces as 30cm and 35cm and the vertical height of the mould is 14cm. So, first of all as given the diameter of the upper and bottom circular surface of the frustum are 35cm and 30cm therefore we have to convert the given diameters into radius.
Now, to find the quantity of molasses that can be poured into it by finding the volume of the mould. So, to find the quantity of molasses we have to find the volume of frustum with the help of the formula as given below:

Formula used: Volume of frustum $ = \dfrac{\pi }{3}({r_1}^2 + r_2^2 + {r_1}{r_2})h.....................(1)$
Where ${r_1}$ is the radius of the upper surface of the vessel and ${r_2}$ is the bottom radius of the vessel and h is the height of the vessel.
Hence, after finding the volume of vessel like frustum shape we have to find the mass of the
molasses as given that each $c{m^3}$of the molasses has mass about 1.2gm, so by multiplying the volume of the vessel we can obtain the mass of the molasses that can be poured into each mould.

Complete step-by-step answer:

Given:
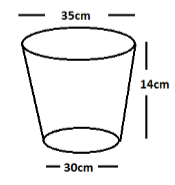
Diameter of the upper surface of the vessel is ${d_1}$= 35cm
Diameter of the bottom surface of the vessel is ${d_2}$= 30cm
Height of the vessel is h = 14cm
Step 1: First of all as given moulds in the shape of a frustum of a cone having the diameter of it’s two circular faces as 30cm and 35cm which are the diameter of the upper and bottom surface of the vessel so we have to find the radius of the upper and bottom surface of the vessel.
Radius of the upper surface of the vessel ${r_1}$= $\dfrac{{{d_1}}}{2}$
Hence,
${r_1}$$ = \dfrac{{35}}{2}$cm
Step 2: Same as the step 1 we have to find the radius of the bottom surface of the vessel.
Radius of the upper surface of the vessel ${r_2} = \dfrac{{{d_2}}}{2}$
Hence,
$
{r_2} = \dfrac{{30}}{2}cm \\
{r_2} = 15cm \\
$
Step 3: Now, to find the quantity of molasses that can be poured into it we have to find the volume of the vessel in shape like frustum with the help of the formula (1) as mentioned in the solution step.
On substituting all the values in the formula (1)
Volume of the mould$ = \dfrac{\pi }{3}\left( {{{15}^2} + {{17.5}^2} + 15 \times 17.5} \right) \times 14c{m^3}$
On substituting the value of $\left( {\pi = \dfrac{{22}}{7}} \right)$as given in the question,
$
= \dfrac{1}{3} \times \dfrac{2}{7}\left( {225 + 306.25 + 262.5} \right)c{m^3} \\
= \dfrac{{44}}{3}\left( {793.75} \right)c{m^3} \\
= \dfrac{{34925}}{3}c{m^3} \\
$
Step 4: Now, as given in the question, mass of the molasses of each $c{m^3}$of the molasses has mass about 1.2gm, so by multiplying the volume of the vessel we can obtain the mass of the molasses that can be poured into each mould.
$
= \dfrac{{34925}}{3} \times 1.2gm \\
= \dfrac{{34925 \times 0.4}}{{1000}}kg \\
= 13.97kg \\
$

Hence, with the help of the formula (1) as mentioned in the solution hint we have obtained the mass of the molasses that can be poured into each mould which is $ = 13.97kg$

Note: Don’t forget to convert the upper and bottommost diameter of the vessel into radius with the help of the formula as radius $ = \dfrac{{diameter}}{2}$
Radius ${r_1}$ can be treated as the outer radius of the given vessel and radius ${r_2}$ can
be taken as the inner radius of the given vessel.
To convert the obtained mass into kg to gm we have to divide it by 1000 because as we
know that $1gm = \dfrac{1}{{1000}}kg$