
How do you graph $y=\sin \left( \theta \right)$ ?
Answer
562.8k+ views
Hint: From the given equation $y=\sin \left( \theta \right)$, try to find some values of ‘y’ corresponding to ‘$\theta $’. Put the values on a table. Using those values plot the graph and do the further analysis if necessary.
Complete step-by-step solution:
$y=\sin \left( \theta \right)$ is a trigonometric function.
For the graph of $y=\sin \left( \theta \right)$, we have to find some ‘y’ values for some corresponding ‘$\theta $’ values.
For some common values of ‘$\theta $’, ‘y’ can be calculated as follows
When $\theta =0$, $y=\sin 0=0$
When $\theta =\pm \dfrac{\pi }{2}$, $y=\sin \left( \pm \dfrac{\pi }{2} \right)=\pm 1$
When $\theta =\pm \pi $, $y=\sin \left( \pm \pi \right)=0$
When $\theta =\pm \dfrac{3\pi }{2}$, $y=\sin \left( \pm \dfrac{3\pi }{2} \right)=\pm 1$
When $\theta =\pm 2\pi $, $y=\sin \left( \pm 2\pi \right)=0$
And so on….
The above data can be collected in a table form as
Using the above values of ‘y’ and ‘$\theta $’, the graph can be drawn as
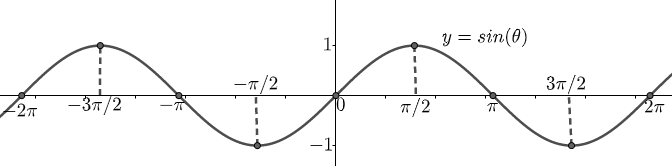
From the above graph, we can conclude that the graph crosses the ‘x’- axis at $\sin \left( \theta \right)=0$. So, the zeros of $y=\sin \left( \theta \right)$ are the multiples of ‘$\pi $’. $\sin \left( \theta \right)$ has the maximum value of 1 and the minimum value of $-1$ at the positive and negative odd multiplier of $\dfrac{\pi }{2}$ respectively.
This is the required solution.
Note: When the values of a function regularly repeat themselves, we say that the function is periodic. From the above graph we can notice that the values of $\sin \left( \theta \right)$ regularly repeat themselves in every $2\pi $ units. Therefore $\sin \left( \theta \right)$ is a periodic function with period ‘$2\pi $’. Since $\sin \left( -\theta \right)=-\sin \left( \theta \right)$, hence $y=\sin \left( \theta \right)$ is an odd function which is symmetrical with respect to the origin.
Complete step-by-step solution:
$y=\sin \left( \theta \right)$ is a trigonometric function.
For the graph of $y=\sin \left( \theta \right)$, we have to find some ‘y’ values for some corresponding ‘$\theta $’ values.
For some common values of ‘$\theta $’, ‘y’ can be calculated as follows
When $\theta =0$, $y=\sin 0=0$
When $\theta =\pm \dfrac{\pi }{2}$, $y=\sin \left( \pm \dfrac{\pi }{2} \right)=\pm 1$
When $\theta =\pm \pi $, $y=\sin \left( \pm \pi \right)=0$
When $\theta =\pm \dfrac{3\pi }{2}$, $y=\sin \left( \pm \dfrac{3\pi }{2} \right)=\pm 1$
When $\theta =\pm 2\pi $, $y=\sin \left( \pm 2\pi \right)=0$
And so on….
The above data can be collected in a table form as
| $\theta $ | 0 | $\pm \dfrac{\pi }{2}$ | $\pm \pi $ | $\pm \dfrac{3\pi }{2}$ | $\pm 2\pi $ |
| y | 0 | $\pm 1$ | 0 | $\pm 1$ | 0 |
Using the above values of ‘y’ and ‘$\theta $’, the graph can be drawn as

From the above graph, we can conclude that the graph crosses the ‘x’- axis at $\sin \left( \theta \right)=0$. So, the zeros of $y=\sin \left( \theta \right)$ are the multiples of ‘$\pi $’. $\sin \left( \theta \right)$ has the maximum value of 1 and the minimum value of $-1$ at the positive and negative odd multiplier of $\dfrac{\pi }{2}$ respectively.
This is the required solution.
Note: When the values of a function regularly repeat themselves, we say that the function is periodic. From the above graph we can notice that the values of $\sin \left( \theta \right)$ regularly repeat themselves in every $2\pi $ units. Therefore $\sin \left( \theta \right)$ is a periodic function with period ‘$2\pi $’. Since $\sin \left( -\theta \right)=-\sin \left( \theta \right)$, hence $y=\sin \left( \theta \right)$ is an odd function which is symmetrical with respect to the origin.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




