Question

How do you graph $ y=-\cot \left( 4\pi x \right) $ ?

Answer 1

Hint: To graph $ y=-\cot \left( 4\pi x \right) $ , we first of all must know how $ y=\cot x $ is graphed. Now, there are two differences between $ \cot x\And (-\cot \left( 4\pi x \right) $ . Firstly, the points where $ \cot x\And (-\cot \left( 4\pi x \right) $ are not defined is different and also the points where they are zero is also different. Another point of difference is that there is a negative sign with $ -\cot \left( 4\pi x \right) $ which will change the nature of the curve which $ \cot x $ has. So, first of all we will find the points where $ -\cot \left( 4\pi x \right) $ is not defined and 0 and then draw the curve in the same way as $ \cot x $ . Now, to compensate for the negative sign in $ -\cot \left( 4\pi x \right) $ we will take the mirror image of the curve so formed in the line mirror of x axis.

Complete step by step answer:
The function that we have to draw is as follows:
 $ y=-\cot \left( 4\pi x \right) $
We know that $ \cot x $ is not defined when:
 $ x=0,\pi ,2\pi ,3\pi ,4\pi ,5\pi ..... $
Using the above information, we can find the points where $ -\cot \left( 4\pi x \right) $ is not defined are:
 $ 4\pi x=0,\pi ,2\pi ,3\pi ,4\pi ,5\pi ...... $
Dividing $ 4\pi $ on both the sides we get,
 $ \begin{align}
  & x=0,\dfrac{\pi }{4\pi },\dfrac{2\pi }{4\pi },\dfrac{3\pi }{4\pi },\dfrac{4\pi }{4\pi },\dfrac{5\pi }{4\pi }.... \\
 & \Rightarrow x=0,\dfrac{1}{4},\dfrac{1}{2},\dfrac{3}{4},\dfrac{1}{1},\dfrac{5}{4}.... \\
\end{align} $
Hence, we have got the points where $ -\cot \left( 4\pi x \right) $ is not defined.
Now, we know that the points where $ \cot x $ is 0 when:
 $ x=\dfrac{\pi }{2},\dfrac{3\pi }{2},\dfrac{5\pi }{2},\dfrac{7\pi }{2}..... $
Using the above points, we can find the points where $ -\cot \left( 4\pi x \right) $ is 0.
 $ 4\pi x=\dfrac{\pi }{2},\dfrac{3\pi }{2},\dfrac{5\pi }{2},\dfrac{7\pi }{2}..... $
Dividing $ 4\pi $ on both the sides we get,
 $ \begin{align}
  & x=\dfrac{\pi }{2\left( 4\pi \right)},\dfrac{3\pi }{2\left( 4\pi \right)},\dfrac{5\pi }{2\left( 4\pi \right)},\dfrac{7\pi }{2\left( 4\pi \right)}..... \\
 & \Rightarrow x=\dfrac{1}{8},\dfrac{3}{8},\dfrac{5}{8},\dfrac{7}{8}.... \\
\end{align} $
Hence, we got the points where $ -\cot \left( 4\pi x \right) $ is 0.
We know the curve for $ \cot x $ as follows:

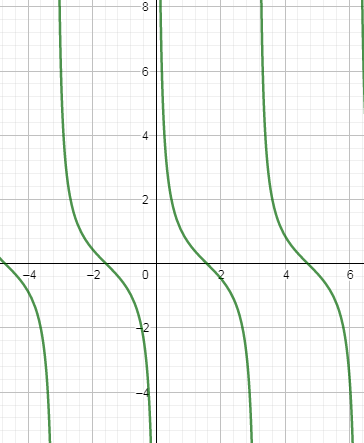
As you can see that $ \cot x $ is not defined at $ x=0,\pi ,2\pi ,3\pi ,4\pi ,5\pi ..... $ and it attains value 0 at $ x=\dfrac{\pi }{2},\dfrac{3\pi }{2},\dfrac{5\pi }{2},\dfrac{7\pi }{2}..... $ . Now, we are going to draw $ \cot \left( 4\pi x \right) $ by retaining the nature of the curve as same as $ \cot x $ but the difference is the points where the function is not defined and 0.

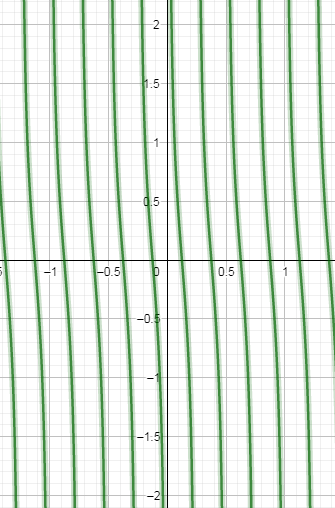
From the above curve, it is clearly shown that the curve is not defined at $ x=0,\dfrac{1}{4},\dfrac{1}{2},\dfrac{3}{4},\dfrac{1}{1},\dfrac{5}{4}.... $ and the curve has value 0 at $ x=\dfrac{1}{8},\dfrac{3}{8},\dfrac{5}{8},\dfrac{7}{8}.... $
Now, to draw the curve $ -\cot \left( 4\pi x \right) $ we have to take the mirror image of the above curve in which the mirror is placed on x axis so the above curve will look in the following way:

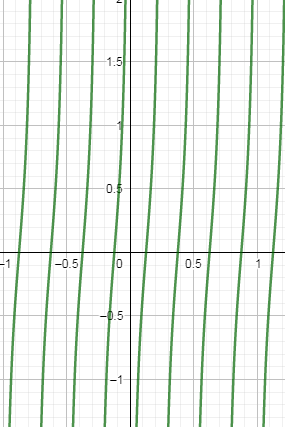
As you can see the nature of the curve is changed with respect to $ \cot x $ .
Hence, the graph of $ -\cot \left( 4\pi x \right) $ is shown below:

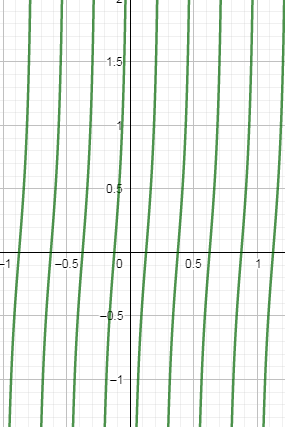
Note:
There are two points where you can make mistakes in drawing the above function.
First, is you forgot to consider the angle of $ -\cot \left( 4\pi x \right) $ which is equal to $ 4\pi x $ and you just draw the same curve as $ \cot x $ . Then the points where $ -\cot \left( 4\pi x \right) $ is not defined and 0 will get wrong.
Another mistake is if you forgot to consider the negative sign in $ -\cot \left( 4\pi x \right) $ then your nature of curve will get wrong.
So, make sure you won’t make the above mistakes.