
How do you graph $ y=\cos \left( \dfrac{x}{2} \right) $ ?
Answer
546.6k+ views
Hint: We are going to draw the graph $ y=\cos \left( \dfrac{x}{2} \right) $ using the values of the cosine ratio for some specific angles given in the basic trigonometric concepts given as $ \cos {{0}^{\circ }}=1 $ , $ \cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}=0.86 $ , $ \cos {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}=0.70 $ , $ \cos {{60}^{\circ }}=\dfrac{1}{2}=0.5 $ and $ \cos {{90}^{\circ }}=0 $ . We will reduce these to the form of the given expression and plot the points obtained in the graph and join them to obtain the curve showing the graph.
Complete step by step answer:
For answering this question we need to draw the graph for $ y=\cos \left( \dfrac{x}{2} \right) $ .
From the basics of trigonometry we know that the values of cosine ratio for some specific angles are given as $ \cos {{0}^{\circ }}=1 $ , $ \cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}=0.86 $ , $ \cos {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}=0.70 $ , $ \cos {{60}^{\circ }}=\dfrac{1}{2}=0.5 $ and $ \cos {{90}^{\circ }}=0 $ .
Here by using these values we can say that
When $ x={{0}^{\circ }}=0\text{ radians} $ the value of $ y $ will be $ 1 $
When $ x={{15}^{\circ }}=\dfrac{\pi }{12}\text{ radians} $ the value of $ y $ will be $ 0.86 $
When $ x=\dfrac{{{45}^{\circ }}}{2}=\dfrac{\pi }{8}\text{ radians} $ the value of $ y $ will be $ 0.70 $
When $ x={{30}^{{}^\circ }}=\dfrac{\pi }{6}\text{ radians} $ the value of $ y $ will be $ 0.5 $
When $ x={{45}^{\circ }}=\dfrac{\pi }{4} $ the value of $ y $ will be $ 0 $
Using these values of $ x $ and $ y $ we can plot the graph for $ y=\cos \left( \dfrac{x}{2} \right) $ . The following table will illustrate the values of $ x $ and $ y $ axes. As we are going to use integers as the scale for the axes we need to substitute $ 3.14 $ instead of $ \pi $ .
By marking these points on the graph and joining the curve we will obtain a graph like the following one illustrated below.
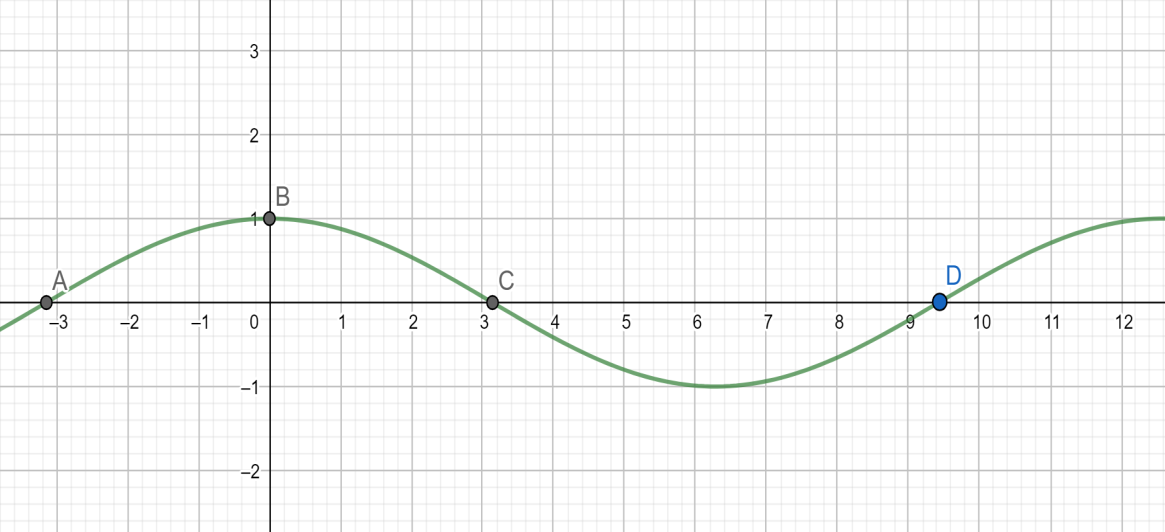
Hence we can conclude that the graph of $ y=\cos \left( \dfrac{x}{2} \right) $ is given as the one shown here.
Note:
We should be sure with the conversions and calculations the accuracy should be maintained in questions of this type. Similarly the graph of $ y=\sin \left( \dfrac{x}{2} \right) $ if we write the values in any one column of the table from bottom to top that is reverse them. This is also a mistake possible if we had forgotten and written them in reverse order by mistake then the curve will not be the same it will differ.
Complete step by step answer:
For answering this question we need to draw the graph for $ y=\cos \left( \dfrac{x}{2} \right) $ .
From the basics of trigonometry we know that the values of cosine ratio for some specific angles are given as $ \cos {{0}^{\circ }}=1 $ , $ \cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}=0.86 $ , $ \cos {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}=0.70 $ , $ \cos {{60}^{\circ }}=\dfrac{1}{2}=0.5 $ and $ \cos {{90}^{\circ }}=0 $ .
Here by using these values we can say that
When $ x={{0}^{\circ }}=0\text{ radians} $ the value of $ y $ will be $ 1 $
When $ x={{15}^{\circ }}=\dfrac{\pi }{12}\text{ radians} $ the value of $ y $ will be $ 0.86 $
When $ x=\dfrac{{{45}^{\circ }}}{2}=\dfrac{\pi }{8}\text{ radians} $ the value of $ y $ will be $ 0.70 $
When $ x={{30}^{{}^\circ }}=\dfrac{\pi }{6}\text{ radians} $ the value of $ y $ will be $ 0.5 $
When $ x={{45}^{\circ }}=\dfrac{\pi }{4} $ the value of $ y $ will be $ 0 $
Using these values of $ x $ and $ y $ we can plot the graph for $ y=\cos \left( \dfrac{x}{2} \right) $ . The following table will illustrate the values of $ x $ and $ y $ axes. As we are going to use integers as the scale for the axes we need to substitute $ 3.14 $ instead of $ \pi $ .
| X | Y |
| 0 | 1 |
| 0.26 | 0.8 |
| 0.39 | 0.7 |
| 0.52 | 0.5 |
| 0.785 | 0 |
By marking these points on the graph and joining the curve we will obtain a graph like the following one illustrated below.

Hence we can conclude that the graph of $ y=\cos \left( \dfrac{x}{2} \right) $ is given as the one shown here.
Note:
We should be sure with the conversions and calculations the accuracy should be maintained in questions of this type. Similarly the graph of $ y=\sin \left( \dfrac{x}{2} \right) $ if we write the values in any one column of the table from bottom to top that is reverse them. This is also a mistake possible if we had forgotten and written them in reverse order by mistake then the curve will not be the same it will differ.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




