
How do you graph $y=\cos \left( \dfrac{1}{2}x \right)+1$?
Answer
537.9k+ views
Hint: First compare the function $y=\cos \left( \dfrac{1}{2}x \right)+1$ with the base function. Find the amplitude, period, phase shift and vertical shift of the function. Then take some different ‘y’ values for corresponding ‘x’ values and plot the graph.
Complete step by step solution:
$y=\cos \left( \dfrac{1}{2}x \right)+1$ is a trigonometric function of the base function $y=\cos x$.
It can be compared to the extended form of the base function $a\cos \left( bx-c \right)+d$, where ‘a’ is the amplitude, ‘b’ is used to find the period, ‘c’ is used to find the phase shift and ‘d’ is the vertical shift.
By comparing, we get
Amplitude $a=1$
$b=\dfrac{1}{2}$
As we know, period$=\dfrac{2\pi }{\left| b \right|}$
So, period$=\dfrac{2\pi }{\dfrac{1}{2}}=2\pi \times \dfrac{2}{1}=4\pi $
$c=0$
Again as we know phase shift$=\dfrac{c}{b}$
So, phase shift$=\dfrac{0}{\dfrac{1}{2}}=0\times \dfrac{2}{1}=0$
Vertical shift $d=1$
For the graph we have to take some different values of ‘y’ for corresponding ‘x’ values
Taking these values of ‘x’ and ‘y’ the graph can be drawn as
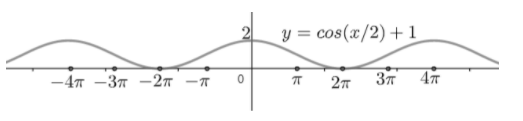
Note:
The base function of $y=\cos \left( \dfrac{1}{2}x \right)+1$ is $y=\cos x$. From the above graph we can conclude that the standard graph of $\cos x$ is shifted up 1 unit on the positive ‘y’- axis with a period, which is extended to $4\pi $. As we know the frequency is the reciprocal of period, so the frequency of the above function will be$=\dfrac{1}{period}=\dfrac{1}{4\pi }$.
Complete step by step solution:
$y=\cos \left( \dfrac{1}{2}x \right)+1$ is a trigonometric function of the base function $y=\cos x$.
It can be compared to the extended form of the base function $a\cos \left( bx-c \right)+d$, where ‘a’ is the amplitude, ‘b’ is used to find the period, ‘c’ is used to find the phase shift and ‘d’ is the vertical shift.
By comparing, we get
Amplitude $a=1$
$b=\dfrac{1}{2}$
As we know, period$=\dfrac{2\pi }{\left| b \right|}$
So, period$=\dfrac{2\pi }{\dfrac{1}{2}}=2\pi \times \dfrac{2}{1}=4\pi $
$c=0$
Again as we know phase shift$=\dfrac{c}{b}$
So, phase shift$=\dfrac{0}{\dfrac{1}{2}}=0\times \dfrac{2}{1}=0$
Vertical shift $d=1$
For the graph we have to take some different values of ‘y’ for corresponding ‘x’ values
| x | 0 | $\pi $ | $2\pi $ | $3\pi $ | $4\pi $ |
| y | 2 | 1 | 0 | 1 | 2 |
Taking these values of ‘x’ and ‘y’ the graph can be drawn as

Note:
The base function of $y=\cos \left( \dfrac{1}{2}x \right)+1$ is $y=\cos x$. From the above graph we can conclude that the standard graph of $\cos x$ is shifted up 1 unit on the positive ‘y’- axis with a period, which is extended to $4\pi $. As we know the frequency is the reciprocal of period, so the frequency of the above function will be$=\dfrac{1}{period}=\dfrac{1}{4\pi }$.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




