Question

How do you graph \[y = {\left( {\dfrac{1}{2}} \right)^x}\] using table of values?

Answer 1

Hint: Since \[x\] is on the right side of the equation, we need to simplify that first. And after that is just straight forward. Just take a bunch of values for \[x\] , then compute the equation by solving to find images of \[y\] by following the rules of the given equation.

Complete step by step solution:
Sometimes tables of values won’t give you hundred percent accuracy because we can’t expect or foresee what happens in the middle of our samples.
In our situation, we first need to simplify our function a little,
By taking the exponent inside the bracket,
 \[y = \dfrac{{{1^x}}}{{{2^x}}}\]
We know that anything to the power of 1 will always become 1 because if we multiply 1 with 1 anytime the result is always 1. So,
 \[y = \dfrac{1}{{{2^x}}}\]
Now we need to take a bunch of values of \[x\] . I’m taking \[ - 3, - 2, - 1,0,1,2,3\] as values
Now if \[x = - 3\] , then
 \[y = \dfrac{1}{{{2^{ - 3}}}}\]
By inverting the exponent and simplifying,
 \[y = 8\]
Now if \[x = - 2\] , then
 \[y = \dfrac{1}{{{2^{ - 2}}}}\]
 \[y = 4\]
By inverting the exponent and simplifying,
Now if \[x = - 1\] , then
 \[y = \dfrac{1}{{{2^{ - 1}}}}\]
By inverting the exponent and simplifying,
 \[y = 2\]
Now if \[x = 0\] , then
 \[y = \dfrac{1}{{{2^0}}}\]
By simplifying,
 \[y = 1\]
Now if \[x = 1\] , then
 \[y = \dfrac{1}{{{2^1}}}\]
By simplifying,
 \[y = \dfrac{1}{2}\]
Now if \[x = 2\] , then
 \[y = \dfrac{1}{{{2^2}}}\]
By simplifying,
 \[y = \dfrac{1}{4}\]
Now if \[x = 3\] , then
 \[y = \dfrac{1}{{{2^3}}}\]
By simplifying,
 \[y = \dfrac{1}{8}\]
By coupling both the values respectively,
We get the following coordinates,
 \[\left( { - 3,8} \right),\left( { - 2,4} \right),\left( { - 1,2} \right),\left( {0,1} \right)\left( {1,\dfrac{1}{2}} \right),\left( {2,\dfrac{1}{4}} \right),\left( {3,\dfrac{1}{8}} \right)\]
Using these we can plot the graph.
Please find the picture in which the graph is plotted using the table of values we found using the given expression.

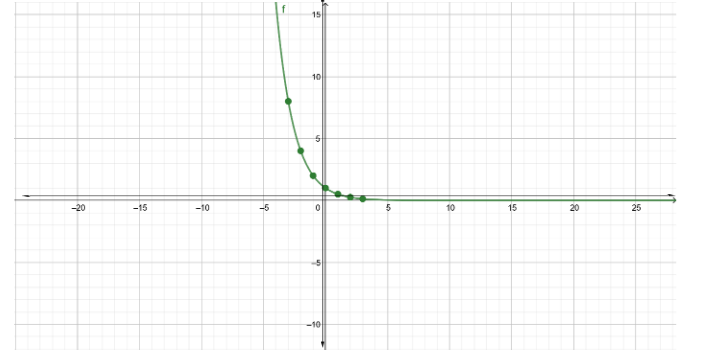
Note: Unfortunately, we can draw the exact graph only for a few functions using a table of values. This concept cannot be used for all the functions because we cannot expect what happens in the middle of our coordinates to plot the graph.