
How do you graph $x+4y=12$ by plotting points?
Answer
531k+ views
Hint: We first find the function of the equation $x+4y=12$. We put the values of $y$ in the function of $x=12-4y$ to find the coordinate form of $\left( x,y \right)$. We put them in the graph to find the line.
Complete step-by-step solution:
We have to graph $x+4y=12$ by plotting points.
We express the equation $x+4y=12$ in the form of a function of $y$ where $f\left( y \right)=x=12-4y$.
We now take the point for $y$ and based on the function $f\left( y \right)=x=12-4y$, we get the values for $x$. We get the coordinates for $\left( x,y \right)$. We plot these points on the graph and then join the points to get the line.
We can take any arbitrary values for $\left( x,y \right)$.
The equation we need to follow is $f\left( y \right)=x=12-4y$.
We have three points in the form of $\left( 4,2 \right)$, $\left( -4,4 \right)$, $\left( 0,3 \right)$.
We plot these points in the graph to get
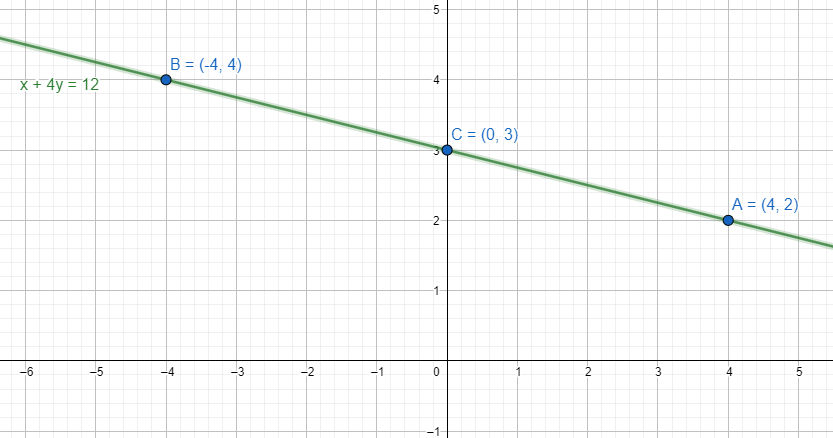
The given line $x+4y=12$ is the line in the graph.
Note: We have to find the x-intercept, and y-intercept of the line $x+4y=12$.
For this we convert the given equation into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$. From the form we get that the x intercept, and y intercept of the line will be $p$ and $q$ respectively. The points will be $\left( p,0 \right),\left( 0,q \right)$.
The given equation is $x+4y=12$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
$\begin{align}
& x+4y=12 \\
& \Rightarrow \dfrac{x}{12}+\dfrac{4y}{12}=1 \\
& \Rightarrow \dfrac{x}{12}+\dfrac{y}{3}=1 \\
\end{align}$
Therefore, the x intercept, and y intercept of the line $x+4y=12$ is 12 and 3 respectively. The axes intersecting points are $\left( 12,0 \right),\left( 0,3 \right)$.
Complete step-by-step solution:
We have to graph $x+4y=12$ by plotting points.
We express the equation $x+4y=12$ in the form of a function of $y$ where $f\left( y \right)=x=12-4y$.
We now take the point for $y$ and based on the function $f\left( y \right)=x=12-4y$, we get the values for $x$. We get the coordinates for $\left( x,y \right)$. We plot these points on the graph and then join the points to get the line.
We can take any arbitrary values for $\left( x,y \right)$.
The equation we need to follow is $f\left( y \right)=x=12-4y$.
| $y$ | 2 | 4 | 3 |
| $x$ | 4 | $-4$ | 0 |
| $\left( x,y \right)$ | $\left( 4,2 \right)$ | $\left( -4,4 \right)$ | $\left( 0,3 \right)$ |
We have three points in the form of $\left( 4,2 \right)$, $\left( -4,4 \right)$, $\left( 0,3 \right)$.
We plot these points in the graph to get

The given line $x+4y=12$ is the line in the graph.
Note: We have to find the x-intercept, and y-intercept of the line $x+4y=12$.
For this we convert the given equation into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$. From the form we get that the x intercept, and y intercept of the line will be $p$ and $q$ respectively. The points will be $\left( p,0 \right),\left( 0,q \right)$.
The given equation is $x+4y=12$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
$\begin{align}
& x+4y=12 \\
& \Rightarrow \dfrac{x}{12}+\dfrac{4y}{12}=1 \\
& \Rightarrow \dfrac{x}{12}+\dfrac{y}{3}=1 \\
\end{align}$
Therefore, the x intercept, and y intercept of the line $x+4y=12$ is 12 and 3 respectively. The axes intersecting points are $\left( 12,0 \right),\left( 0,3 \right)$.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




