
How do you graph using the intercepts for 5x – 5y = 10?
Answer
571.5k+ views
Hint: Here in this question, we will use the general form of the equation of slope and intercept to solve this problem. The general form of this equation is y = mx + c where m is the slope and c is the constant here that tells you to shift up or down the graph by b units. This is basically slope-intercept form which we will be using in this question.
Complete step by step answer:
Now let’s solve the question.
As we know about the slope-intercept form that it is a general form of a straight line and is expressed as y = mx + c where ‘m’ is a slope and c is a constant and intercepts are m and c.
For plotting the straight line, first, we need to convert the given equation in a slope-intercept form. Let’s see how!
Write the equation from the question.
$ \Rightarrow $ 5x - 5y = 10
Take 5 common from the left-hand side:
$ \Rightarrow $ 5(x - y) = 10
Now take 5 to the other side:
$ \Rightarrow $ x – y = $ \dfrac{10}{5} $
$ \Rightarrow $ x – y = 5
Take 5 to the left side and –y to the right side of the equation. We get:
$ \Rightarrow y=x-5.....(i) $
Therefore, we have got our equation in the slope-intercept form i.e. y = mx + c.
Here, m = 1 and c = -5 .
Now, we have to find the intercepts for x and y.
Let’s find y-intercept first. Substitute x = 0 in equation(i) we get:
$ \Rightarrow $ y = (0) - 5
Now we get the value of ‘y’ as:
$ \Rightarrow $ y = -5
$ \therefore $ y-intercept form is: $ \left( 0,-5 \right) $
Similarly, find x-intercept. Put y = 0 in equation(i) we get:
$ \Rightarrow $ (0) = x – 5
Now the value of x will be:
$ \Rightarrow $ x = 5
$ \therefore $ x-intercept will be: (5,0)
Now, let’s plot the graph of the equation given in the question with the help of the intercepts.
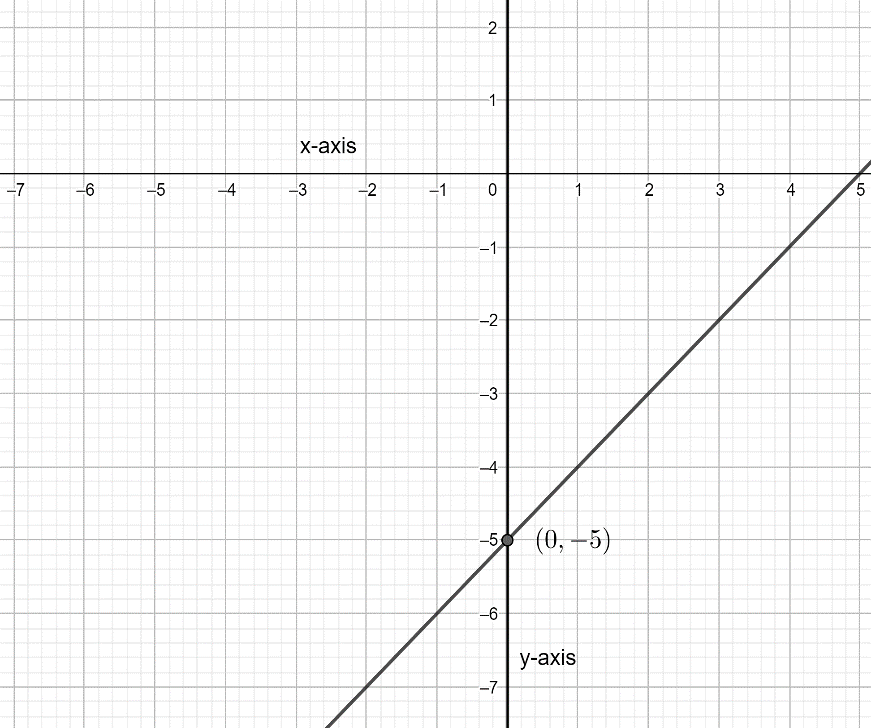
The graph above is of y-intercept: (0,-5)
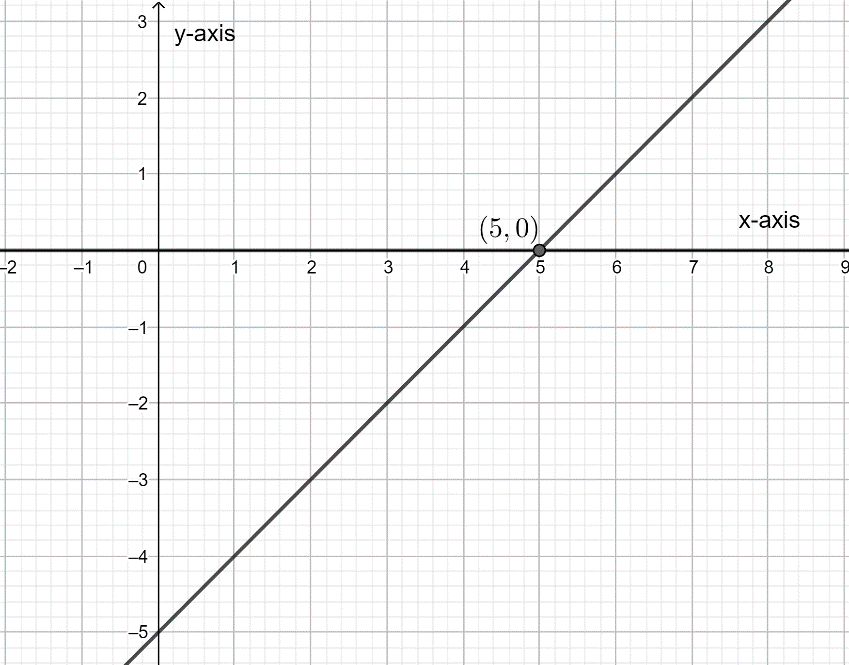
The graph above is of x-intercept: (5,0)
Note:
In this question particularly, we have to use the slope-intercept form as it is asked to graph the equation by using intercepts. Else the question can be solved by substitution also. Plot the graph neatly.
Complete step by step answer:
Now let’s solve the question.
As we know about the slope-intercept form that it is a general form of a straight line and is expressed as y = mx + c where ‘m’ is a slope and c is a constant and intercepts are m and c.
For plotting the straight line, first, we need to convert the given equation in a slope-intercept form. Let’s see how!
Write the equation from the question.
$ \Rightarrow $ 5x - 5y = 10
Take 5 common from the left-hand side:
$ \Rightarrow $ 5(x - y) = 10
Now take 5 to the other side:
$ \Rightarrow $ x – y = $ \dfrac{10}{5} $
$ \Rightarrow $ x – y = 5
Take 5 to the left side and –y to the right side of the equation. We get:
$ \Rightarrow y=x-5.....(i) $
Therefore, we have got our equation in the slope-intercept form i.e. y = mx + c.
Here, m = 1 and c = -5 .
Now, we have to find the intercepts for x and y.
Let’s find y-intercept first. Substitute x = 0 in equation(i) we get:
$ \Rightarrow $ y = (0) - 5
Now we get the value of ‘y’ as:
$ \Rightarrow $ y = -5
$ \therefore $ y-intercept form is: $ \left( 0,-5 \right) $
Similarly, find x-intercept. Put y = 0 in equation(i) we get:
$ \Rightarrow $ (0) = x – 5
Now the value of x will be:
$ \Rightarrow $ x = 5
$ \therefore $ x-intercept will be: (5,0)
Now, let’s plot the graph of the equation given in the question with the help of the intercepts.
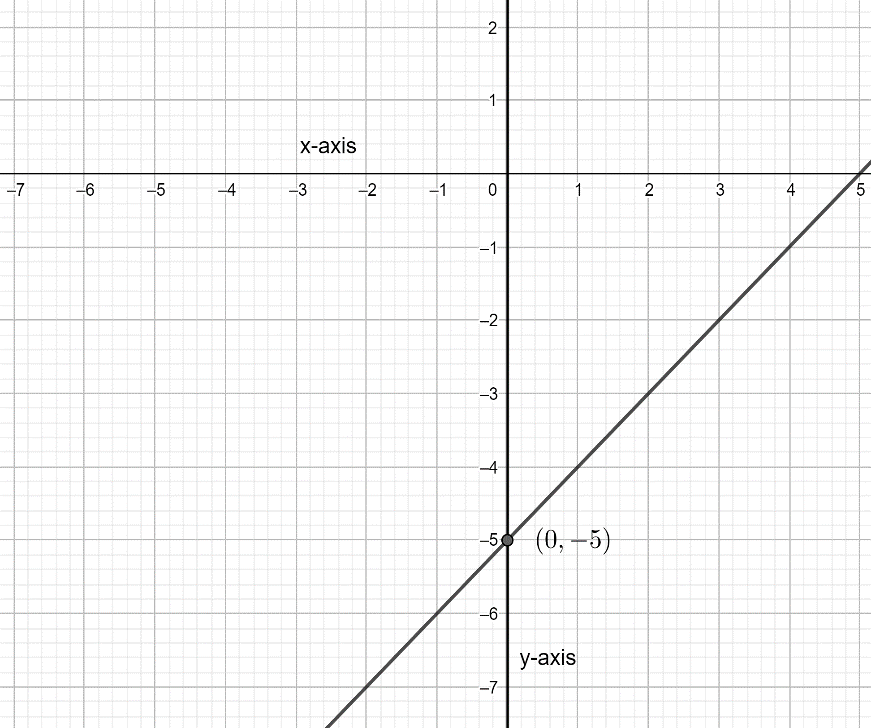
The graph above is of y-intercept: (0,-5)
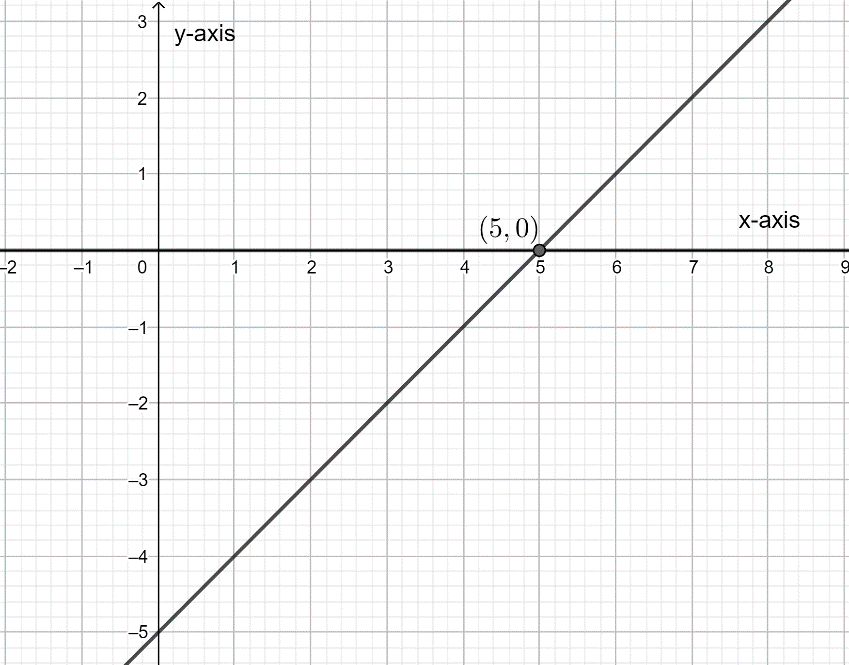
The graph above is of x-intercept: (5,0)
Note:
In this question particularly, we have to use the slope-intercept form as it is asked to graph the equation by using intercepts. Else the question can be solved by substitution also. Plot the graph neatly.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

State and explain Ohms law class 10 physics CBSE

Distinguish between soap and detergent class 10 chemistry CBSE

a Why did Mendel choose pea plants for his experiments class 10 biology CBSE

Draw the diagram of the sectional view of the human class 10 biology CBSE




