Question

Graph the trigonometric equation $ y = 3\cos x $

Answer 1

Hint: If in an equation, there are one or more than one trigonometric ratios [sine $ \left( {\sin } \right) $ , cosine $ \left( {\cos } \right) $ , tangent $ \left( {\tan } \right) $ , cotangent $ \left( {\cot } \right) $ , secant $ \left( {\sec } \right) $ , cosecant $ \left( {\cos ec} \right) $ ] of unknown angles, it is said to be trigonometric equation and here, we have to make a graph of the given trigonometric equation.

Complete step-by-step answer:
To make a graph of the trigonometric equation, we have a function, $ f\left( x \right) = a\cos b\left( {x + c} \right) + d $
On comparing the function $ y = 3\cos x $ with the above function, we have found that only the parameter a, means $ 3 $ will affect our function. Now, let us assume the values of x in the function $ f\left( x \right) $ which is equal to y.
Part-1 Let us assume the value of x be $ 0 $ , then the function $ f\left( x \right) $ becomes,
 $ f\left( 0 \right) = 3\cos \left( 0 \right) = 3 \times 1 = 3 $
And we know that, $ f\left( x \right) = y $ , then the value of y becomes $ 3 $ .
Part-2 Let us assume the value of x be $ \dfrac{\pi }{6} $ , then the function $ f\left( x \right) $ becomes,
 $ f\left( {\dfrac{\pi }{6}} \right) = 3\cos \left( {\dfrac{\pi }{6}} \right) = 3 \times \left( {\dfrac{{\sqrt 3 }}{2}} \right) = \dfrac{{3\sqrt 3 }}{2} $
And we know that, $ f\left( x \right) = y $ , then the value of y becomes $ \dfrac{{3\sqrt 3 }}{2} $ .
Part-3 Let us assume the value of x be $ \dfrac{\pi }{4} $ , then the function $ f\left( x \right) $ becomes,
 $ f\left( {\dfrac{\pi }{4}} \right) = 3\cos \left( {\dfrac{\pi }{4}} \right) = 3 \times \dfrac{1}{{\sqrt 2 }} = \dfrac{3}{{\sqrt 2 }} $
And we know that, $ f\left( x \right) = y $ , then the value of y becomes $ \dfrac{3}{{\sqrt 2 }} $ .
Part-4 Let us assume the value of x be $ \dfrac{\pi }{2} $ , then the function $ f\left( x \right) $ becomes,
 $ f\left( {\dfrac{\pi }{2}} \right) = 3\cos \left( {\dfrac{\pi }{2}} \right) = 3 \times 0 = 0 $
And we know that, $ f\left( x \right) = y $ , then the value of y becomes $ 0 $ .
Part-5 Let us assume the value of x be $ \pi $ , then the function $ f\left( x \right) $ becomes,
 $ f\left( \pi \right) = 3\cos \left( \pi \right) = 3 \times \left( { - 1} \right) = - 3 $
And we know that, $ f\left( x \right) = y $ , then the value of y becomes $ - 3 $ .
Hence, we have our values of x and y to plot the graph of $ y = 3\cos x $ and the graph is,

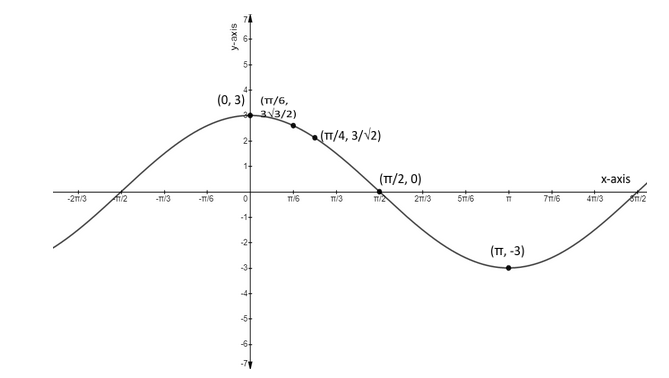
Note: To form a graph of cosine function, there is an equation i.e, $ f\left( x \right) = a\cos b\left( {x + c} \right) + d $ , where, a is the amplitude of the function, b affects the period as it is equal to $ \dfrac{{2\pi }}{b} $ , if the value of b increases then the value of period decreases, c is the horizontal shift and d is the principal axis. The graph of the given trigonometric equation is quite easy to solve as only $ 3 $ is affecting the function.