
How do you graph the solution to \[\left( {x + 4} \right)\left( {x - 6} \right) > 0\] on a number line?
Answer
558k+ views
Hint: In these types of questions as the given inequalities should be factored and the given factors should be tested in the ranges and the intervals should satisfy the given inequality and finally the intervals should be plotted on the graph.
Complete step-by-step answer:
Given inequality is \[\left( {x + 4} \right)\left( {x - 6} \right) > 0\],
Now we will multiply both the terms and equate the result to zero to find the critical point of x,
\[\left( {x + 4} \right)\left( {x - 6} \right) > 0\]
Now multiplying and equate it 0, we get,
\[{x^2} + 4x - 6x - 24 = 0\],
Now factorising we get,
\[{x^2} + 2x - 24 = 0\],
So, now we get,
\[\left( {x + 4} \right)\left( {x - 6} \right) = 0\],
Now we get the critical points of x we get,
\[x + 4 = 0\], or \[x - 6 = 0\],
Now set factors to zero we get,
\[x = - 4\], and
\[x = 6\],
Now check the intervals in between the critical points, i.e., test the intervals to see if they satisfy the given inequality.
Let’s check \[x < - 4\], let us take any value in the range, let us take \[x = - 5\], we get
\[\left( { - 5 + 4} \right)\left( { - 5 - 6} \right) > 0\],
By simplifying we get,
\[\left( { - 1} \right)\left( { - 11} \right) > 0\],
By multiplying we get,
\[11 > 0\], satisfy the given inequality,
Now let us check the range \[ - 4 < x < 6\], now we will take a value between the ranges let us take 2, we will get,
\[\left( {2 + 4} \right)\left( {2 - 6} \right) > 0\],
Now multiplying we get,
\[\left( 6 \right)\left( { - 4} \right) > 0\],
Again by simplifying we get,
\[ - 24 > 0\], which doesn’t satisfy the given inequality.
Now let us check the range \[x > 6\], let us take a value In the range, so let us take 7, we will get,
\[\left( {x + 4} \right)\left( {x - 6} \right) > 0\],
Now substitute \[x = 7\] in the equality we get,
\[\left( {7 + 4} \right)\left( {7 - 6} \right) > 0\],
Now multiplying we get,
\[\left( {11} \right)\left( 1 \right) > 0\],
Now again simplifying we get,
\[11 > 0\], which satisfies the given inequality.
So the required solution for the given inequality is \[x < - 4\] or \[x > 6\].
Now plotting the solution on the graph we get,
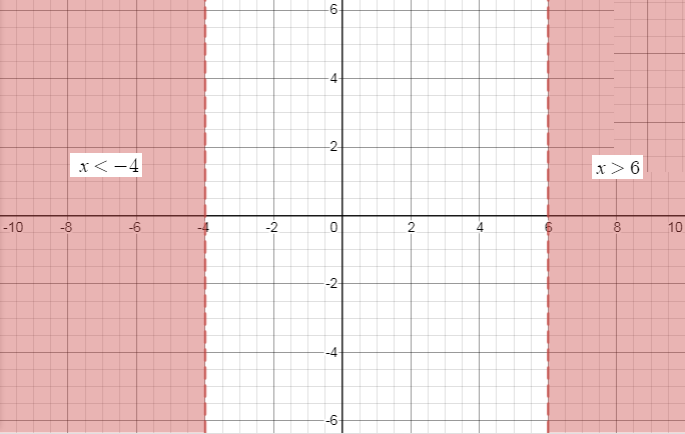
Final Answer:
The required graph of the given inequality \[\left( {x + 4} \right)\left( {x - 6} \right) > 0\] is,
Note:
While solving these types of questions we should be careful in calculations as there is a chance of making a mistake in the calculations, and should plot the intervals on the number line.
Complete step-by-step answer:
Given inequality is \[\left( {x + 4} \right)\left( {x - 6} \right) > 0\],
Now we will multiply both the terms and equate the result to zero to find the critical point of x,
\[\left( {x + 4} \right)\left( {x - 6} \right) > 0\]
Now multiplying and equate it 0, we get,
\[{x^2} + 4x - 6x - 24 = 0\],
Now factorising we get,
\[{x^2} + 2x - 24 = 0\],
So, now we get,
\[\left( {x + 4} \right)\left( {x - 6} \right) = 0\],
Now we get the critical points of x we get,
\[x + 4 = 0\], or \[x - 6 = 0\],
Now set factors to zero we get,
\[x = - 4\], and
\[x = 6\],
Now check the intervals in between the critical points, i.e., test the intervals to see if they satisfy the given inequality.
Let’s check \[x < - 4\], let us take any value in the range, let us take \[x = - 5\], we get
\[\left( { - 5 + 4} \right)\left( { - 5 - 6} \right) > 0\],
By simplifying we get,
\[\left( { - 1} \right)\left( { - 11} \right) > 0\],
By multiplying we get,
\[11 > 0\], satisfy the given inequality,
Now let us check the range \[ - 4 < x < 6\], now we will take a value between the ranges let us take 2, we will get,
\[\left( {2 + 4} \right)\left( {2 - 6} \right) > 0\],
Now multiplying we get,
\[\left( 6 \right)\left( { - 4} \right) > 0\],
Again by simplifying we get,
\[ - 24 > 0\], which doesn’t satisfy the given inequality.
Now let us check the range \[x > 6\], let us take a value In the range, so let us take 7, we will get,
\[\left( {x + 4} \right)\left( {x - 6} \right) > 0\],
Now substitute \[x = 7\] in the equality we get,
\[\left( {7 + 4} \right)\left( {7 - 6} \right) > 0\],
Now multiplying we get,
\[\left( {11} \right)\left( 1 \right) > 0\],
Now again simplifying we get,
\[11 > 0\], which satisfies the given inequality.
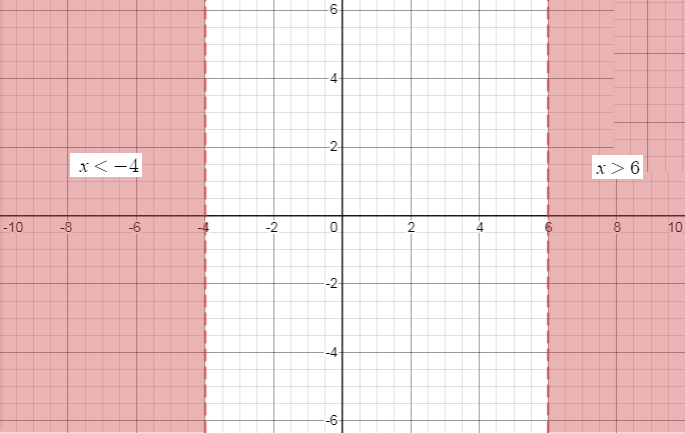
So the required solution for the given inequality is \[x < - 4\] or \[x > 6\].
Now plotting the solution on the graph we get,

Final Answer:
The required graph of the given inequality \[\left( {x + 4} \right)\left( {x - 6} \right) > 0\] is,

Note:
While solving these types of questions we should be careful in calculations as there is a chance of making a mistake in the calculations, and should plot the intervals on the number line.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




