
How do you graph the inequality \[x < - 4\] on the coordinate plane ?
Answer
552.6k+ views
Hint:First we need to draw the graph of the equation\[x = - 4\] . We use intercept form to draw the graph. That is we find the coordinate of the given equation lying on the line of x- axis, we can find this by substituting the value of ‘y’ is equal to zero (x-intercept). Similarly we can find the coordinate of the equation lying on the line of y- axis, we can find this by substituting the value of ‘x’ equal to zero (y-intercept). After drawing the graph we can check in which region the inequality satisfies. Here if we draw \[x < - 4\] we will have a parallel line to the y-axis.
Complete step by step answer:
Given, \[x < - 4\]. Now consider \[x = - 4\].
For \[x = - 4\].
Here we don’t have a ‘y’ variable in the given equation. So ‘x’ will always equal to \[ - 4\], no matter what value we put in for ‘y’, the ‘x’ is always going to be \[ - 4\]. That is,
Let’s plot a graph for these coordinates. We take scale x-axis= 1 unit = 1 units and y-axis= 1 unit = 1 units.
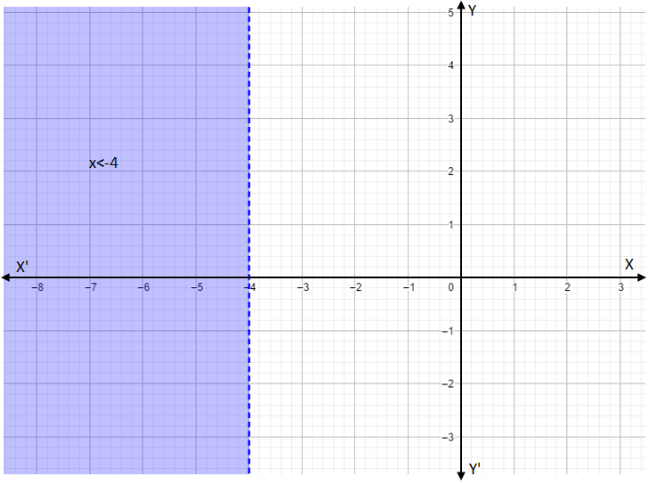
For \[x < - 4\], we can see in the graph that we have a straight vertical line that crosses the x axis at \[ - 4\]. The solution is all the coordinate points left to the line \[x = - 4\]. If we take coordinate points right to the line the inequality won’t be satisfied. In the above graph the shaded region is the solution of the given inequality.
Note:We don’t take points lying on the line \[x = - 4\] for the inequality \[x < - 4\]. A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.
Complete step by step answer:
Given, \[x < - 4\]. Now consider \[x = - 4\].
For \[x = - 4\].
Here we don’t have a ‘y’ variable in the given equation. So ‘x’ will always equal to \[ - 4\], no matter what value we put in for ‘y’, the ‘x’ is always going to be \[ - 4\]. That is,
| \[x\] | \[ - 4\] | \[ - 4\] | \[ - 4\] | \[ - 4\] | \[ - 4\] | \[ - 4\] | \[ - 4\] | \[ - 4\] |
| \[y\] | \[1\] | \[ - 1\] | \[2\] | \[ - 2\] | \[3\] | \[ - 3\] | \[4\] | \[ - 4\] |
Let’s plot a graph for these coordinates. We take scale x-axis= 1 unit = 1 units and y-axis= 1 unit = 1 units.

For \[x < - 4\], we can see in the graph that we have a straight vertical line that crosses the x axis at \[ - 4\]. The solution is all the coordinate points left to the line \[x = - 4\]. If we take coordinate points right to the line the inequality won’t be satisfied. In the above graph the shaded region is the solution of the given inequality.
Note:We don’t take points lying on the line \[x = - 4\] for the inequality \[x < - 4\]. A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Explain zero factorial class 11 maths CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

A solution of a substance X is used for white washing class 11 chemistry CBSE




