Question

How do you graph the given function $ r=5\sin 5\theta $ ?

Answer 1

Hint: We start solving the problem by finding the maximum and minimum values of the function using the fact that the values of the function $ a\sin bx $ lies in the interval $ \left[ -a,a \right] $ . We then make use of the fact that the maximum value of the function $ a\sin bx $ occurs at $ bx=\left( 4n+1 \right)\dfrac{\pi }{2} $ , $ n\in \mathbb{Z} $ to find the values of $ \theta $ at which we get the maximum values of the given function. We then make use of the fact that that the minimum value of the function $ a\sin bx $ occurs at $ bx=\left( 4n-1 \right)\dfrac{\pi }{2} $ , $ n\in \mathbb{Z} $ to find the values of $ \theta $ at which we get the minimum values of the given function. We then make use of the fact that that the function $ a\sin bx $ is equal to 0 at $ bx=n\pi $ , $ n\in \mathbb{Z} $ to find the values of $ \theta $ at which the given function is equal to 0. We then plot all the obtained points to get the required graph.

Complete step by step answer:
According to the problem, we are asked to plot the given function $ r=5\sin 5\theta $ on a graph.
So, we have the function $ r=5\sin 5\theta $ ---(1).
We know that the values of the function $ a\sin bx $ lies in the interval $ \left[ -a,a \right] $ .
So, the values of the function $ r=5\sin 5\theta $ lies in the interval $ \left[ -5,5 \right] $ .
We know that the maximum value of the function $ a\sin bx $ occurs at $ bx=\left( 4n+1 \right)\dfrac{\pi }{2} $ , $ n\in \mathbb{Z} $ .
So, the maximum value of the function $ r=5\sin 5\theta $ occurs at $ 5\theta =\left( 4n+1 \right)\dfrac{\pi }{2}\Leftrightarrow \theta =\left( 4n+1 \right)\dfrac{\pi }{10} $ , $ n\in \mathbb{Z} $ ---(1).
We know that the minimum value of the function $ a\sin bx $ occurs at $ bx=\left( 4n-1 \right)\dfrac{\pi }{2} $ , $ n\in \mathbb{Z} $ .
So, the minimum value of the function $ r=5\sin 5\theta $ occurs at $ 5\theta =\left( 4n-1 \right)\dfrac{\pi }{2}\Leftrightarrow \theta =\left( 4n-1 \right)\dfrac{\pi }{10} $ , $ n\in \mathbb{Z} $ ---(2).
We know that the function $ a\sin bx $ is equal to 0 at $ bx=n\pi $ , $ n\in \mathbb{Z} $ .
So, the value of the function $ r=5\sin 5\theta $ is 0 at $ 5\theta =n\pi \Leftrightarrow \theta =\dfrac{n\pi }{5} $ , $ n\in \mathbb{Z} $ ---(3).
Now, let us plot the points obtained at all the points obtained from equations (1), (2), and (3) to get the required graph which is as shown below.

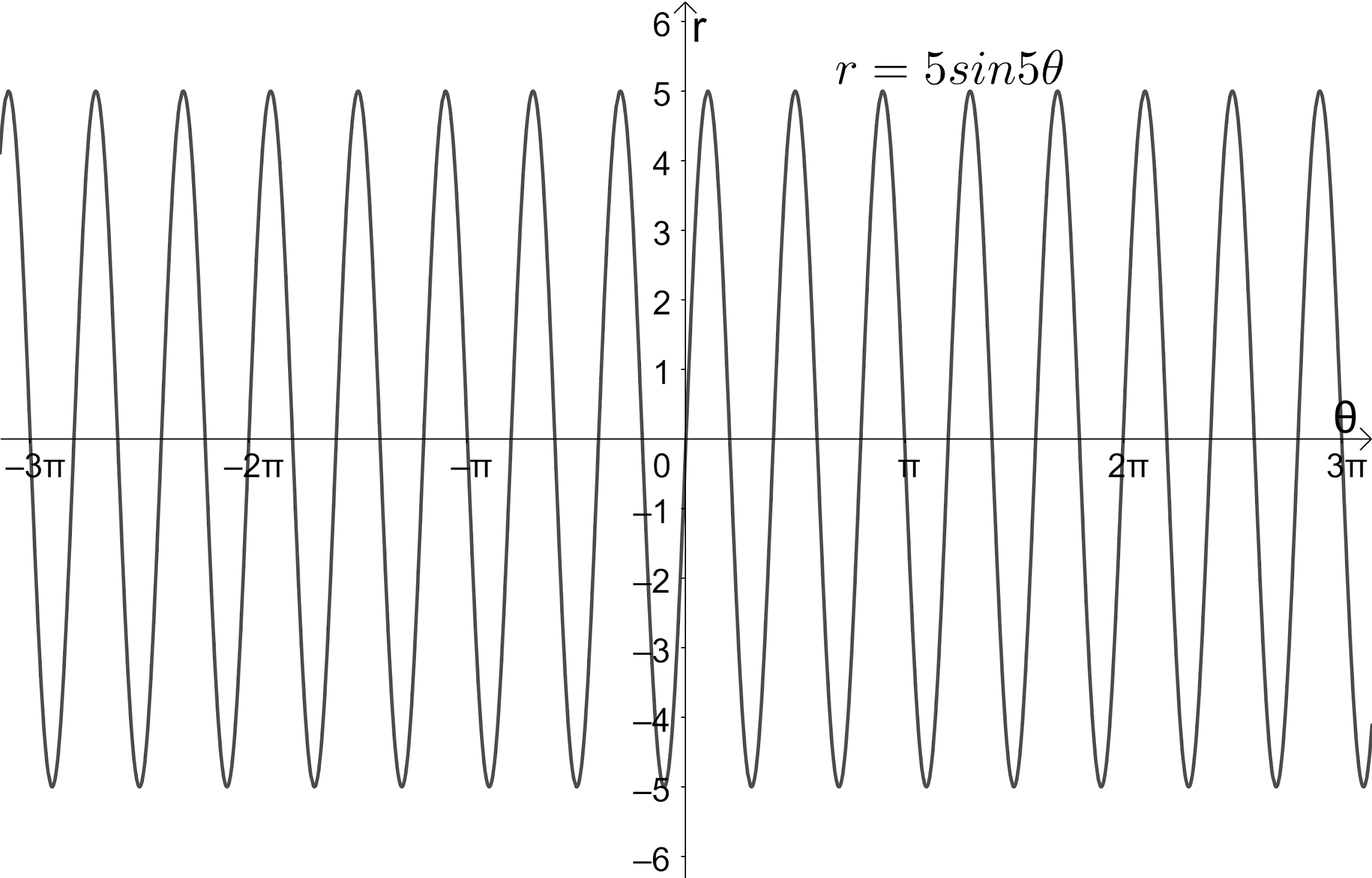
Note:
We should not confuse the general solution for the minimum and maximum values of the function $ a\sin bx $ as this will give the wrong graph for us. Whenever we get this type of problem, we first find the points at which we get the minimum, maximum, and 0 to plot the graph. Similarly, we can expect problems to plot the graph of the function $ r=3\cos 6\theta +3\sin 4\theta $.