Question

How do you graph the function $y = - x + 9$ ?

Answer 1

Hint: Start by finding the slope and y-intercept. A function can be represented on a graph if both the input and output are real numbers. On the x-axis, we plot the inputs and on the y axis, we plot the outputs. Next, find two ordered pairs for the given equation. After that draw x-axis and y-axis on the graph paper and mark the points. Finally, check whether all the points lie on the same line.

Complete step by step answer:
Given the function $y = - x + 9$ .
Let us start by solving for $y$ .
We know that the slope-intercept form is $y = mx + b$ , where $m$ is the slope, and $b$ is the y-intercept.
So here the slope is $- 1$ and the y-intercept is $9$ .
Next to find the $x$ and $y$ coordinates, substitute two values for $x$ in the given equation. That is, first assume that $x = 0$ . Then it can be written as,
$y = - \left( 0 \right) + 9$
$y = 9$
Next assume $y = 0$ , then,
$0 = - x + 9$
$x = 9$
Hence, when $x = 0$ then $y=9$ and when $x = 9$ then $y = 0$ .
Therefore we can graph the function using the $x$ and $y$ coordinates as shown below.

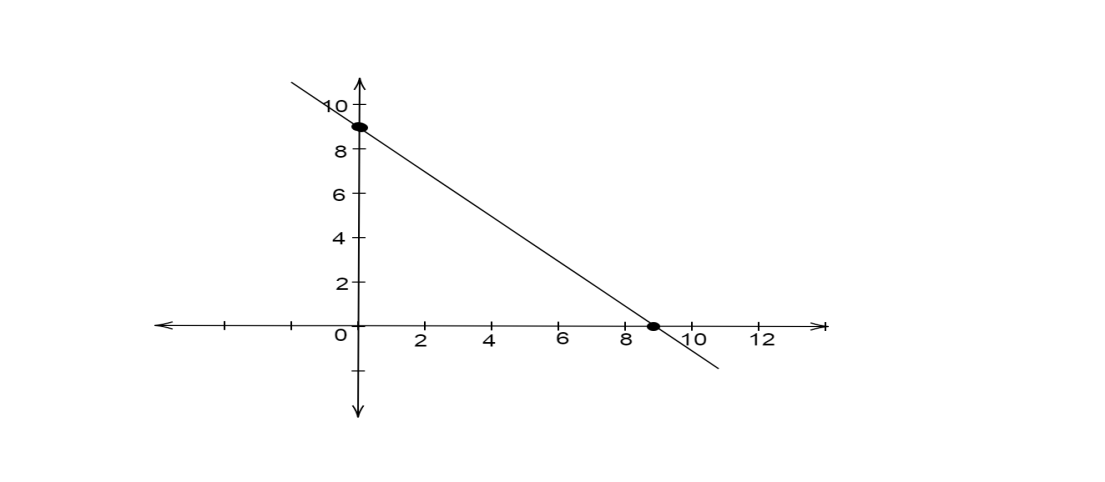
Note: Always remember that in the case of a linear equation in two variables the graph will be a straight line. A minimum of two ordered pairs should be found for drawing the graph. If possible it is always advised to find four ordered pairs to draw the graph. Also, remember that $y = mx + b$ where $m$ is the slope and $b$ is the y-intercept is known as the slope-intercept form. The graph can either be created using the slope and y-intercept values or using the ordered pairs obtained.