
Graph the function \[y = \cos 2x\]?
Answer
565.2k+ views
Hint: In this question, first we have to find the period and amplitude of the given function, and then take some values for \[x\] and then find the respective \[y\] for each \[x\], then tabulate the values and with help of the table we will get the required graph.
Complete step-by-step answer:
The graph of \[y = \cos x \] is like a wave that forever oscillates between. \[ - 1\] and \[1\], in a shape that repeats itself every \[2\pi \] units. Specifically, this means that the domain of \[\cos x\] is all real numbers, and the range is \[\left[ { - 1,1} \right]\].
Now given function is \[y = \cos 2x\],
Use the form \[y = a\sin \left( {bx - c} \right) + d\] to find the variables used to find the amplitude, period, phase shift, and vertical shift.
\[a = 1\],\[b = 2\],\[c = 0\], and \[d = 0\],
So here amplitude \[a = 1\],
Now period of the function is given by, \[\dfrac{{2\pi }}{{\left| b \right|}}\] from the given data,
So, substituting the value of \[b = 2\] in the period formula, we get,
\[ \Rightarrow \dfrac{{2\pi }}{{\left| 2 \right|}} = \pi \],
Period of the given function will be \[\pi \],
Now select some values to graph the function,
When \[x = 0\],
\[ \Rightarrow \]\[y = \cos 2x\],
Now simplifying we get,
\[ \Rightarrow y = \cos 2\left( 0 \right)\],
Now simplifying we get,
\[y = \cos 0 = 1\]
When \[x = \dfrac{\pi }{2}\],
\[ \Rightarrow y = \cos 2\left( {\dfrac{\pi }{2}} \right)\],
Now simplifying we get,
\[ \Rightarrow y = \cos \pi = - 1\],
When \[x = \pi \],
\[ \Rightarrow y = \cos 2\left( \pi \right)\],
Now simplifying we get,
\[ \Rightarrow y = \cos 2\pi = 1\],
When \[x = \dfrac{{3\pi }}{2}\],
\[ \Rightarrow y = \cos 2\left( {\dfrac{{3\pi }}{2}} \right)\],
Now simplifying we get,
\[ \Rightarrow y = \cos 3\pi = - 1\],
When \[x = 2\pi \],
\[ \Rightarrow y = \cos 2\left( {2\pi } \right)\],
Now simplifying we get,
\[ \Rightarrow y = \cos 4\pi = 1\],
Now tabulating the values we get,
Now plotting the graphs we get,
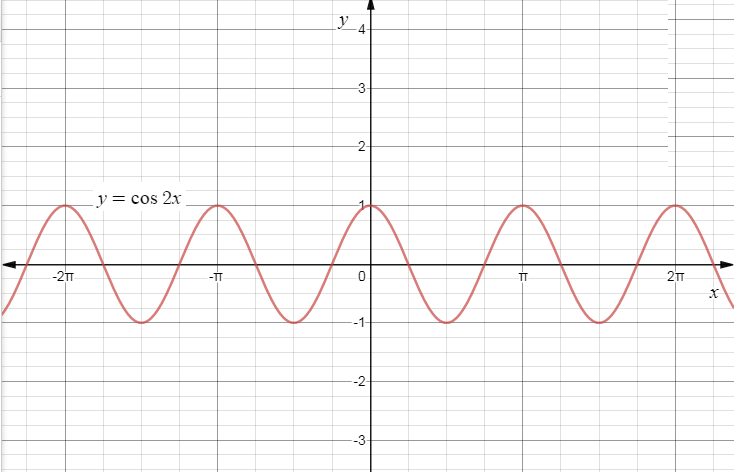
\[\therefore \]The required graph for the function \[y = \cos 2x\] is,
Note:
To graph the cosine function, we mark the angle along the horizontal x axis, and for each angle, we put the cosine of that angle on the vertical y-axis. The graph, as seen above, is a smooth curve that varies from +1 to -1. It is the same shape as the cosine function but displaced to the left \[{90^o}\]. Curves that follow this shape are called 'sinusoidal' after the name of the sine function whose shape it resembles.
Complete step-by-step answer:
The graph of \[y = \cos x \] is like a wave that forever oscillates between. \[ - 1\] and \[1\], in a shape that repeats itself every \[2\pi \] units. Specifically, this means that the domain of \[\cos x\] is all real numbers, and the range is \[\left[ { - 1,1} \right]\].
Now given function is \[y = \cos 2x\],
Use the form \[y = a\sin \left( {bx - c} \right) + d\] to find the variables used to find the amplitude, period, phase shift, and vertical shift.
\[a = 1\],\[b = 2\],\[c = 0\], and \[d = 0\],
So here amplitude \[a = 1\],
Now period of the function is given by, \[\dfrac{{2\pi }}{{\left| b \right|}}\] from the given data,
So, substituting the value of \[b = 2\] in the period formula, we get,
\[ \Rightarrow \dfrac{{2\pi }}{{\left| 2 \right|}} = \pi \],
Period of the given function will be \[\pi \],
Now select some values to graph the function,
When \[x = 0\],
\[ \Rightarrow \]\[y = \cos 2x\],
Now simplifying we get,
\[ \Rightarrow y = \cos 2\left( 0 \right)\],
Now simplifying we get,
\[y = \cos 0 = 1\]
When \[x = \dfrac{\pi }{2}\],
\[ \Rightarrow y = \cos 2\left( {\dfrac{\pi }{2}} \right)\],
Now simplifying we get,
\[ \Rightarrow y = \cos \pi = - 1\],
When \[x = \pi \],
\[ \Rightarrow y = \cos 2\left( \pi \right)\],
Now simplifying we get,
\[ \Rightarrow y = \cos 2\pi = 1\],
When \[x = \dfrac{{3\pi }}{2}\],
\[ \Rightarrow y = \cos 2\left( {\dfrac{{3\pi }}{2}} \right)\],
Now simplifying we get,
\[ \Rightarrow y = \cos 3\pi = - 1\],
When \[x = 2\pi \],
\[ \Rightarrow y = \cos 2\left( {2\pi } \right)\],
Now simplifying we get,
\[ \Rightarrow y = \cos 4\pi = 1\],
Now tabulating the values we get,
| \[x\] | \[y\] |
| 0 | 1 |
| \[\dfrac{\pi }{2}\] | -1 |
| \[\pi \] | 1 |
| \[\dfrac{{3\pi }}{2}\] | -1 |
| \[2\pi \] | 1 |
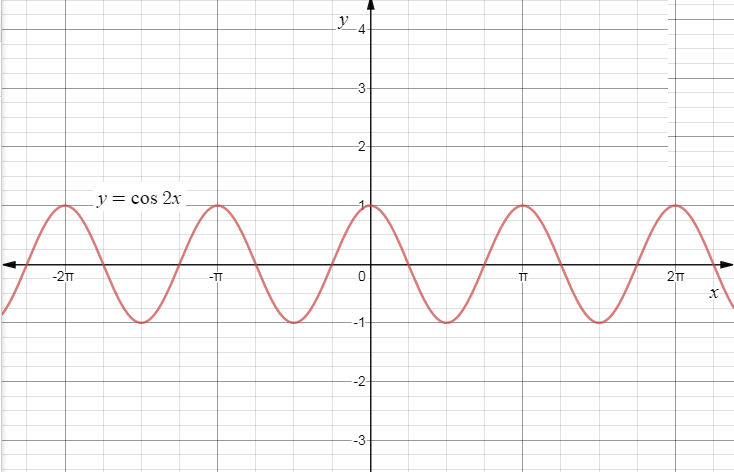
Now plotting the graphs we get,

\[\therefore \]The required graph for the function \[y = \cos 2x\] is,

Note:
To graph the cosine function, we mark the angle along the horizontal x axis, and for each angle, we put the cosine of that angle on the vertical y-axis. The graph, as seen above, is a smooth curve that varies from +1 to -1. It is the same shape as the cosine function but displaced to the left \[{90^o}\]. Curves that follow this shape are called 'sinusoidal' after the name of the sine function whose shape it resembles.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




