Question

How do I graph the function of \[r = \cos 2\theta \] ?

Answer 1

Hint: Here in this question, we have to plot the graph of the given trigonometric equation. To plot the graph first we have to find the coordinate \[\left( {r,\theta } \right)\] by comparing the general equation of the rose curve i.e., \[r = a\cos \left( {n\theta } \right)\] . By finding the coordinate we can plot the required graph of given trigonometric equation

Complete step by step solution:
In general let we consider \[r = a\cos \left( {n\theta } \right)\] or \[r = a\sin (n\theta )\] where \[a \ne 0\] and n is a positive number greater than 1. For the graph of rose if the value of n is odd then rose will have n petals or if the value of n is even then the rose will have 2n petals. Here “a” represents the radius of the circle where the rose petals lies.
Now consider the given equation \[r = \cos 2\theta \] . Here a=1, the radius of circle is 1 and n=2, the number is even so we have 2n petals i.e., 4 petals for the rose.
Now consider the given equations ------- (1)
Substitute r=0 in equation (1) we have
 \[ \Rightarrow 0 = \cos 2\theta \]
By taking the inverse we have
 \[ \Rightarrow {\cos ^{ - 1}}(0) = 2\theta \]
By the table of trigonometry ratios for standard angles in radians we have \[\cos \left( {\dfrac{{n\pi }}{2}} \right) = 0\] , where n= 1, 3, 5, 7, … then \[{\cos ^{ - 1}}\left( 0 \right) = \dfrac{\pi }{2}\] .
 \[ \Rightarrow \dfrac{\pi }{2} = 2\theta \]
Dividing by 2 on the both sides we have
 \[ \Rightarrow \theta = \dfrac{\pi }{4}\]
Therefore, when \[r = 0\] we have \[\theta = \dfrac{\pi }{4},\dfrac{{3\pi }}{4},\dfrac{{5\pi }}{4},\dfrac{{7\pi }}{4}\]
Similarly:
When \[\theta = 0\] , we have \[r = 0,\dfrac{\pi }{2},\pi ,\dfrac{{3\pi }}{2},2\pi \] .
While determining the area we use the above coordinates
Hence the graph of the given rose curve equation \[r = \cos 2\theta \] is:

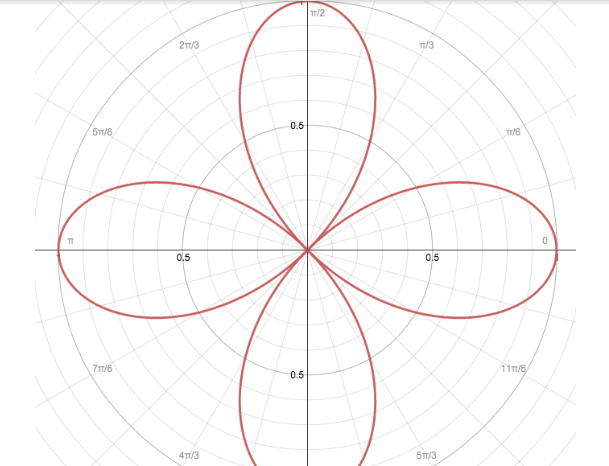
Note: Here we have to plot the polar graph. The polar graph is plotted versus \[r\] and \[\theta \] . By substituting the value of \[\theta \] we can determine the value of \[r\] . Here a=1, the radius of the circle is 1 and n=3, the number is odd so we have 3 petals for the rose. The petals will not exceed the circle of radius.