
How do you graph the function $f(x) = {x^3} - 2$ and its inverses?
Answer
532.2k+ views
Hint: We will first find out any three or more points lying on the graph of $f(x) = {x^3} - 2$. Then, we will put in f (x) = y and find the value of x in terms of y which will be the inverse function and thus we can plot it as well.
Complete step by step solution:
We are given that we are required to graph the function $f(x) = {x^3} - 2$ and its inverses.
Let us find some points which lie on the given equation.
Putting x = 0, we will then obtain the following equation:-
$ \Rightarrow f(0) = {0^3} - 2$
Simplifying the calculations in the above equation, we will then obtain the following equation with us:-
$ \Rightarrow f(0) = - 2$
Putting x = 1, we will then obtain the following equation:-
$ \Rightarrow f(1) = {1^3} - 2$
Simplifying the calculations in the above equation, we will then obtain the following equation with us:-
$ \Rightarrow f(1) = - 1$
Putting x = - 1, we will then obtain the following equation:-
$ \Rightarrow f( - 1) = - {1^3} - 2$
Simplifying the calculations in the above equation, we will then obtain the following equation with us:-
$ \Rightarrow f( - 1) = - 3$
Thus, we have the following table:-
Plotting these and joining these points by curve, we will then obtain the following equation:-
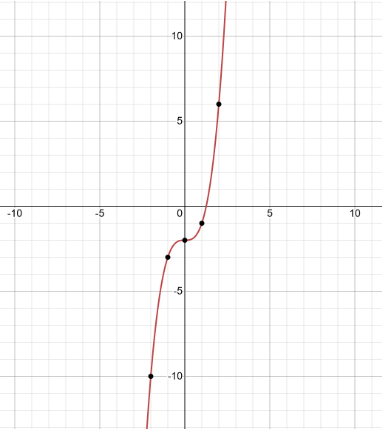
Now let us put in $f(x) = y$, we will then obtain the following equation:-
$ \Rightarrow y = {x^3} - 2$
Taking 2 from subtraction in the right hand side to addition in the left hand side, we will then obtain the following equation:-
$ \Rightarrow y + 2 = {x^3}$
Taking the cube root on both the sides, we will obtain the following equation:-
$ \Rightarrow x = \sqrt[3]{{y + 2}}$
Putting back $f(x) = y$, we have:-
$ \Rightarrow {f^{ - 1}}(y) = \sqrt[3]{{y + 2}}$
Replacing y by x, we have:-
$ \Rightarrow {f^{ - 1}}(x) = \sqrt[3]{{x + 2}}$
Thus, we have the inverse function as well.
We will see which points lie on this graph:-
Plotting this graph, we get:-
Thus, we have the required graphs.
Note:
The students must note that we have found the inverse of the function and then found the points lying on it that way only.
We have the following function with us:-
$ \Rightarrow x = \sqrt[3]{{y + 2}}$
Putting is y = - 1, then we will get x = 1
Putting in y = - 2, then we will get x = 0
Putting in y = 6, we will then get x = 2
Thus, we have the points as we saw in the above solution.
Inverse of the function is just the rotation of the normal graph of the function, if you may notice the graph of both the equations.
Complete step by step solution:
We are given that we are required to graph the function $f(x) = {x^3} - 2$ and its inverses.
Let us find some points which lie on the given equation.
Putting x = 0, we will then obtain the following equation:-
$ \Rightarrow f(0) = {0^3} - 2$
Simplifying the calculations in the above equation, we will then obtain the following equation with us:-
$ \Rightarrow f(0) = - 2$
Putting x = 1, we will then obtain the following equation:-
$ \Rightarrow f(1) = {1^3} - 2$
Simplifying the calculations in the above equation, we will then obtain the following equation with us:-
$ \Rightarrow f(1) = - 1$
Putting x = - 1, we will then obtain the following equation:-
$ \Rightarrow f( - 1) = - {1^3} - 2$
Simplifying the calculations in the above equation, we will then obtain the following equation with us:-
$ \Rightarrow f( - 1) = - 3$
Thus, we have the following table:-
| $x$ | 0 | 1 | -1 |
| $f(x)$ | -2 | -1 | -3 |
Plotting these and joining these points by curve, we will then obtain the following equation:-

Now let us put in $f(x) = y$, we will then obtain the following equation:-
$ \Rightarrow y = {x^3} - 2$
Taking 2 from subtraction in the right hand side to addition in the left hand side, we will then obtain the following equation:-
$ \Rightarrow y + 2 = {x^3}$
Taking the cube root on both the sides, we will obtain the following equation:-
$ \Rightarrow x = \sqrt[3]{{y + 2}}$
Putting back $f(x) = y$, we have:-
$ \Rightarrow {f^{ - 1}}(y) = \sqrt[3]{{y + 2}}$
Replacing y by x, we have:-
$ \Rightarrow {f^{ - 1}}(x) = \sqrt[3]{{x + 2}}$
Thus, we have the inverse function as well.
We will see which points lie on this graph:-
| $y$ | -2 | -1 | 6 |
| $x$ | 0 | 1 | 2 |
Plotting this graph, we get:-

Thus, we have the required graphs.
Note:
The students must note that we have found the inverse of the function and then found the points lying on it that way only.
We have the following function with us:-
$ \Rightarrow x = \sqrt[3]{{y + 2}}$
Putting is y = - 1, then we will get x = 1
Putting in y = - 2, then we will get x = 0
Putting in y = 6, we will then get x = 2
Thus, we have the points as we saw in the above solution.
Inverse of the function is just the rotation of the normal graph of the function, if you may notice the graph of both the equations.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




