Question

How do you graph the exponential function $ y = {2^x} + 1? $

Answer 1

Hint: First find the domain (x values) and the range (y values) of the given exponential function $ y = {2^x} + 1 $ , exponential graphs are always increasing exponentially if their base is greater than one and are always decreasing exponentially if the base is greater than zero but less than one, keep this in mind when plotting the graph and point the domain and range accordingly.

Complete step-by-step answer:
In order to plot graph of an exponential equation or function, we first need to find the value of its domain and the range.
So finding the values of domain and the range of the given function $ y = {2^x} + 1 $
We know that the domain of an exponential function belongs to set of numbers, i.e. $ ( - \infty ,\;\infty ) $
Putting left limit of the domain in the equation to find the value of range,
 $
   \Rightarrow \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } ({2^x} + 1) \\
   \Rightarrow \mathop {\lim }\limits_{x \to - \infty } y = 0 + 1 \\
  \mathop { \Rightarrow \lim }\limits_{x \to - \infty } y = 1 \\
  $
Again putting right hand limit to find upper value of the range,
 $
   \Rightarrow \mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } ({2^x} + 1) \\
   \Rightarrow \mathop {\lim }\limits_{x \to - \infty } y = \infty + 1 \\
  \mathop { \Rightarrow \lim }\limits_{x \to - \infty } y = \infty \\
  $
Therefore range of the equation $ y = {2^x} + 1 $ is given as $ [1,\;\infty ) $
And at $ x = 0,\;y = {2^0} + 1 = 1 + 1 = 2 $ ,
That is at $ x = 0 $ graph will pass from $ y = 2 $
Since the base of the exponent in the given function is $ 2 $ which is neither negative nor less than $ 1 $
Therefore graph will be always increasing,

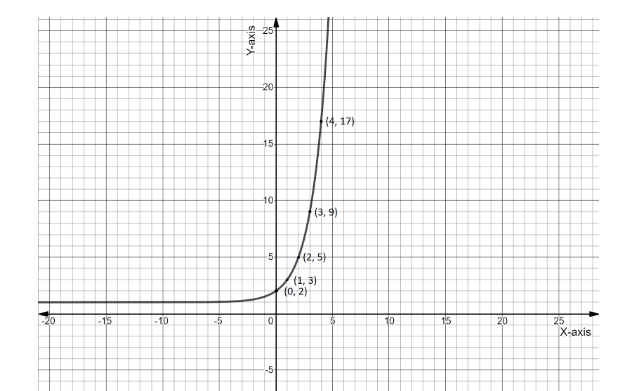
This is the required graph for the equation $ y = {2^x} + 1 $

Note: While plotting the graph don’t touch the minimum range of the equation (minimum “y” value), because that’s not the actual minimum value of the equation, since $ {2^{ - \infty }} $ is tends to zero, not actually zero.
Sometimes, higher domain value of function gives left limit of the range whereas lower domain value gives right limit of range, this happens because of the decreasing nature of equation, so keep the nature of equation in mind when finding range.