Question

How do you graph parametric equations?

Answer 1

Hint: The parametric equations are used to represent an implicit relation between the Cartesian variables x and y, each of which is explicitly expressed in terms of another variable, say t. Therefore, the parametric equations will always be a pair of equations, in which x and y variables are equated to some functions of t. For graphing the parametric equations, we need to eliminate the parameter t from the relations for x and y so as to obtain an explicit relation between these. We can take up the example of graphing the parametric equations given by $x=t-2$ and $y={{t}^{2}}$.

Complete step by step solution:
The parametric equations are the pair of equations in terms of a parameter t which represent an implicit relation between the variables x and y. Let us consider an example of the parametric equations given by
\[\begin{align}
  & \Rightarrow x=t-2.........\left( i \right) \\
 & \Rightarrow y={{t}^{2}}........\left( ii \right) \\
\end{align}\]
For graphing the parametric equations, we need to eliminate the parameter t so as to obtain an explicit relation between x and y. Therefore, considering the equation (i) we have
$\Rightarrow x=t-2$
Adding $2$ both the sides, we get
$\begin{align}
  & \Rightarrow x+2=t-2+2 \\
 & \Rightarrow x+2=t \\
 & \Rightarrow t=x+2 \\
\end{align}$
Substituting the above equation in the equation (ii) we get
$\Rightarrow y={{\left( x+2 \right)}^{2}}$
The graph of the above equation can be shown as below.

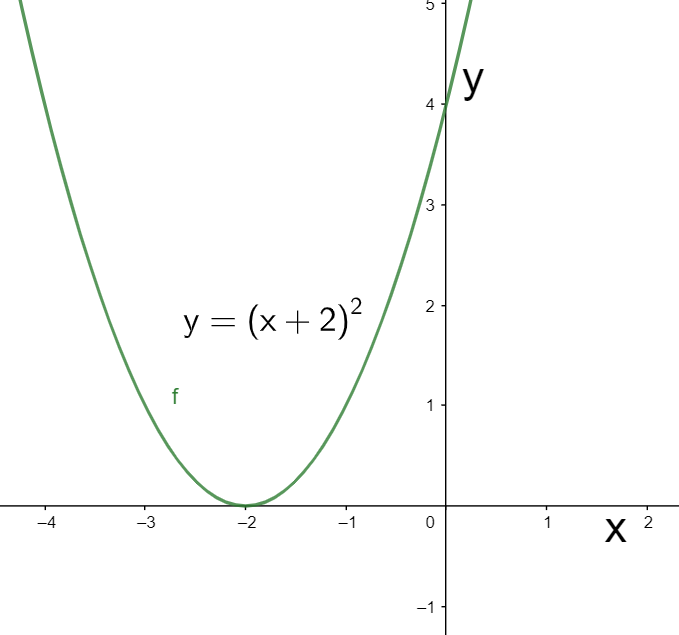
Hence, we have graphed the parametric equations $x=t-2$ and $y={{t}^{2}}$.

Note: The parametric equations, in some cases, may be unsolvable to obtain an explicit relation between x and y. In such cases, we are needed to make a table of values of x and y for the discrete values of t. But we must note that the graph obtained will not be smooth in such cases.