Question

How is the graph of \[f(x) = x{}^2 - \,4\] related to that of \[f(x) = x{}^2\] ?

Answer 1

Hint: The above question is related to the transformation of graphs. The original graph of the equation \[f(x) = x{}^2\] is an upward opening parabola with vertex at origin. In the new equation \[f(x) = x{}^2 - \,4\] ,the function change is along the y-axis. The remaining nature of the parabola remains the same. Thus it is only required to shift the vertex of the original equation to obtain the new one.

Complete step-by-step answer:
The function \[f(x) = x{}^2 - \,4\] can be written as \[{x^2} = f(x) + 4\] and the function \[f(x) = x{}^2\] can be written as \[{x^2} = f(x)\] . Now the function \[{x^2} = f(x)\] represents an upward opening parabola with its vertex at origin. Now, if we compare the second equation \[{x^2} = f(x) + 4\] with the first one, we can see that that the left hand side of both the equations are same but the right hand side of second equation is 4 units less than the previous one.
Therefore, the equation \[f(x) = x{}^2 - \,4\] can be obtained by shifting the equation \[f(x) = x{}^2\] four units in the downward direction. Hence the graph is transformed as below.

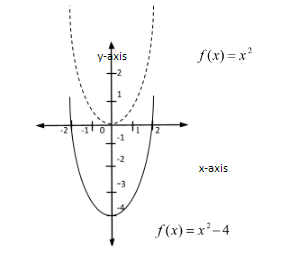
Hence we can observe that the graph of the equation \[f(x) = x{}^2 - \,4\] can be obtained by shifting the graph of the equation \[f(x) = x{}^2\] along the y-axis in the negative direction.

Note: There are some basic graphical transformations of parabolas which are to be noted. The function \[f(x) = x{}^2 + b\] has a graph which simply looks like the standard parabola \[f(x) = x{}^2\] with its vertex shifted \[b\,\,units\] along the y-axis. Thus the vertex will be located at \[(0,b)\] . if \[b\] is a positive value then the parabola moves \[b\,units\] upwards and if the value of \[b\] is negative then the parabola moves \[b\,\,units\] downward. Another form of parabola has the equation \[f(x) = {(x - a)^2}\] which has the graph same of that of \[f(x) = x{}^2\] with its vertex shifted \[a\,\,units\] along x-axis. If \[a\] is positive it shifts \[a\,\,units\] to the right and if the value of \[a\] is negative it shifts \[a\,\,units\] to the left .The the vertex of the parabola changes to \[(a,0)\] .
These two types of transformation can be combined to produce a parabola which is congruent to the basic parabola but with vertex at \[(a,b)\] .