Question

How do you graph line through the point \[\left( {5, - 3} \right)\] with undefined slope?

Answer 1

Hint: If the slope of a line is undefined, then the line is a vertical line, so it cannot be written in slope-intercept form, but it can be written in the form: \[x = a\], where a is a constant. Here, the line has an undefined slope and passes through the point \[\left( {5, - 3} \right)\], then the equation of the line is at \[x = 5\].

Complete step by step solution:
The line with undefined slope means that the line is parallel to the y-axis (If we measure its slope, then you would get division by zero which is undefined)
The equation of the line is \[x = a\], where a is the value of the x-coordinates that the line passes through.
In this case it passes through\[\left( {5, - 3} \right)\]hence\[x = 5\] is the equation.
To graph plot \[\left( {5, - 3} \right)\], \[\left( {5,1} \right)\] and so on any point with \[x = 5\].
Here is the graph of \[x = 5\].

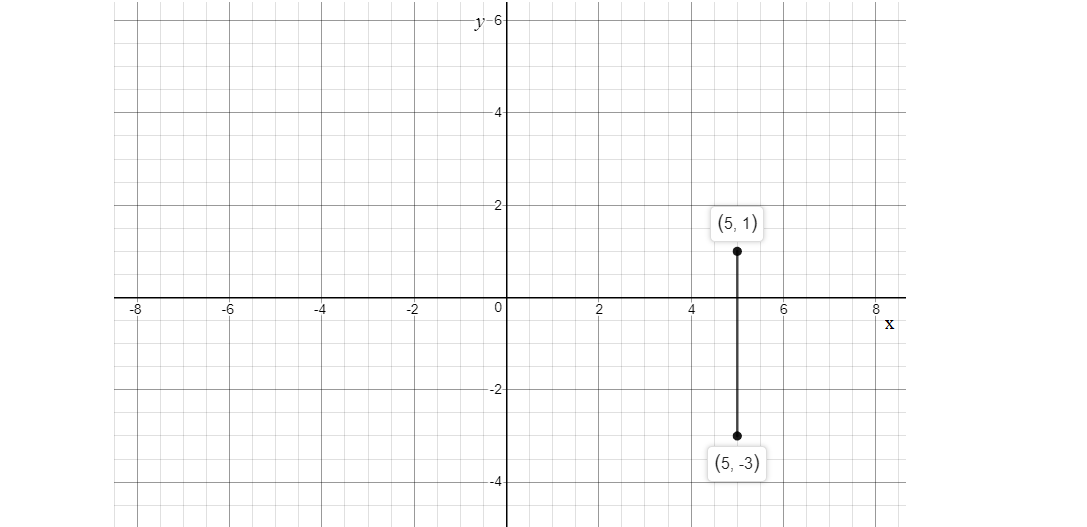
As shown above, the graph line through the point \[\left( {5, - 3} \right)\], is a vertical line as the slope of the line is undefined.


Note: The key point to note is that, if the slope of the line is undefined, then, by definition the line is a vertical line. Since we did not have a change in the x values, the denominator of our slope is 0. This means that we have an undefined slope. The slope of a line characterizes the direction of a line and to find the slope, you divide the difference of the y-coordinates of two points on a line by the difference of the x-coordinates of those same two points.