
How do you graph \[f(x) = 6x\] by plotting points?
Answer
541.2k+ views
Hint: We need to draw the graph ‘x’ versus ‘y’. Here we treat f(x) as . Normally we give the random values for ‘x’ and we find the value of ‘y’. If we give all the real number values of ‘x’ we will get a decimal point of ‘y’ which is difficult to point out the coordinate in the graph. So we give all the real values for ‘y’ and we find the ‘x’ values. Thus we will have coordinate points (x, y). Hence, we can plot the graph by using the values. We can also draw the graph using the intercept method. But here we have a function which is passing through origin. So we use tables to draw the graph.
Complete step-by-step solution:
Given \[f(x) = 6x\].
That is we have \[y = 6x\]
Let's give the values for ‘x’ and we find the value of ‘y’.
Put \[x = 1\]in \[y = 6x\] we have,
\[y = 6 \times 1 = 6\]
Thus we have coordinate points \[(1,6)\].
Put \[x = 1\]in \[y = 6x\] we have,
\[y = 6 \times - 1 = - 6\]
Thus we have coordinate point \[( - 1, - 6)\].
Put \[x = 2\]in \[y = 6x\] we have,
\[y = 6 \times 2 = 12\]
Thus we have coordinate points \[(2,12)\].
Put \[x = - 2\]in \[y = 6x\] we have,
\[y = 6 \times - 2 = - 12\]
Thus we have coordinate point \[( - 2, - 12)\].
Put \[x = 3\]in \[y = 6x\] we have,
\[y = 6 \times 3 = 18\]
Thus we have coordinate points \[(3,18)\].
Put \[x = - 3\]in \[y = 6x\] we have,
\[y = 6 \times - 3 = - 18\]
Thus we have coordinate points \[( - 3, - 18)\].
Let’s draw the graph for these coordinates,
Here we take x-axis = 1 unit = 5units
y-axis = 1 unit =1 unit.
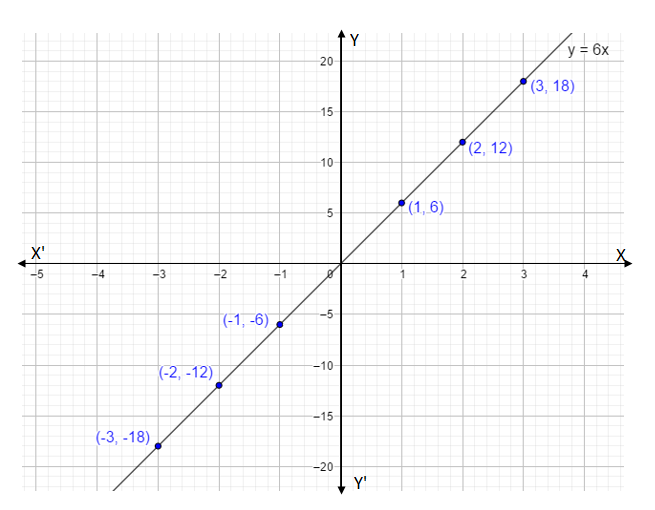
Note: We can see that the given curve is parabola. A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations
Complete step-by-step solution:
Given \[f(x) = 6x\].
That is we have \[y = 6x\]
Let's give the values for ‘x’ and we find the value of ‘y’.
Put \[x = 1\]in \[y = 6x\] we have,
\[y = 6 \times 1 = 6\]
Thus we have coordinate points \[(1,6)\].
Put \[x = 1\]in \[y = 6x\] we have,
\[y = 6 \times - 1 = - 6\]
Thus we have coordinate point \[( - 1, - 6)\].
Put \[x = 2\]in \[y = 6x\] we have,
\[y = 6 \times 2 = 12\]
Thus we have coordinate points \[(2,12)\].
Put \[x = - 2\]in \[y = 6x\] we have,
\[y = 6 \times - 2 = - 12\]
Thus we have coordinate point \[( - 2, - 12)\].
Put \[x = 3\]in \[y = 6x\] we have,
\[y = 6 \times 3 = 18\]
Thus we have coordinate points \[(3,18)\].
Put \[x = - 3\]in \[y = 6x\] we have,
\[y = 6 \times - 3 = - 18\]
Thus we have coordinate points \[( - 3, - 18)\].
| \[x\] | \[1\] | \[ - 1\] | \[2\] | \[ - 2\] | \[3\] | \[ - 3\] |
| \[y\] | \[6\] | \[ - 6\] | \[12\] | \[ - 12\] | \[18\] | \[ - 18\] |
Let’s draw the graph for these coordinates,
Here we take x-axis = 1 unit = 5units
y-axis = 1 unit =1 unit.

Note: We can see that the given curve is parabola. A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




