Question

Graph drawn from the equation $$y=x^2-3x-4$$ will be.

Answer 1

Hint: In this question, we have to find out the type of the equation by the graphical representation.
For doing that first we need to consider the points $$x=0,1,2,3$$ putting this in the given equation and find out the coordinates (x,y) and plot in the graphs. Then we need to predict what the graph represents.

Complete step by step answer:
In this question we have to find out the type of the equation by the graphical representation.
The given equation is $$y=x^2-3x-4$$.
Now we need to first graphically plot it, for doing that we need to find out the y coordinates for the x values $$x=0,1,2,3$$…...
Now putting $$x=0$$in the given equation we get,
$$y=-4$$
putting $$x=1$$in the given equation we get,
$$y=1-3-4$$
Solving we get,
$$y=-6$$
Now putting $$x=2$$in the given equation we get,
$$y=2^2-3\times 2-4$$
$$y=4-6-4=-6$$
Now putting $$x=3$$in the given equation we get,
$$y=3^2-3\times 3-4$$
$$y=9-9-4=-4$$
Putting $$y=0$$in the given equation we get,
$$x^2-3x-4=0$$
Solving we get,
$$x^2-4x+x-4=0$$
$$x(x-4)+1(x-4)=0$$
$$(x-4)(x+1)=0$$
$$x=4or,-1$$
Hence the points on the given equation are
$$(0,-4),(1,-6),(2,-6),(3,-4),(4,0),(-1,0)$$

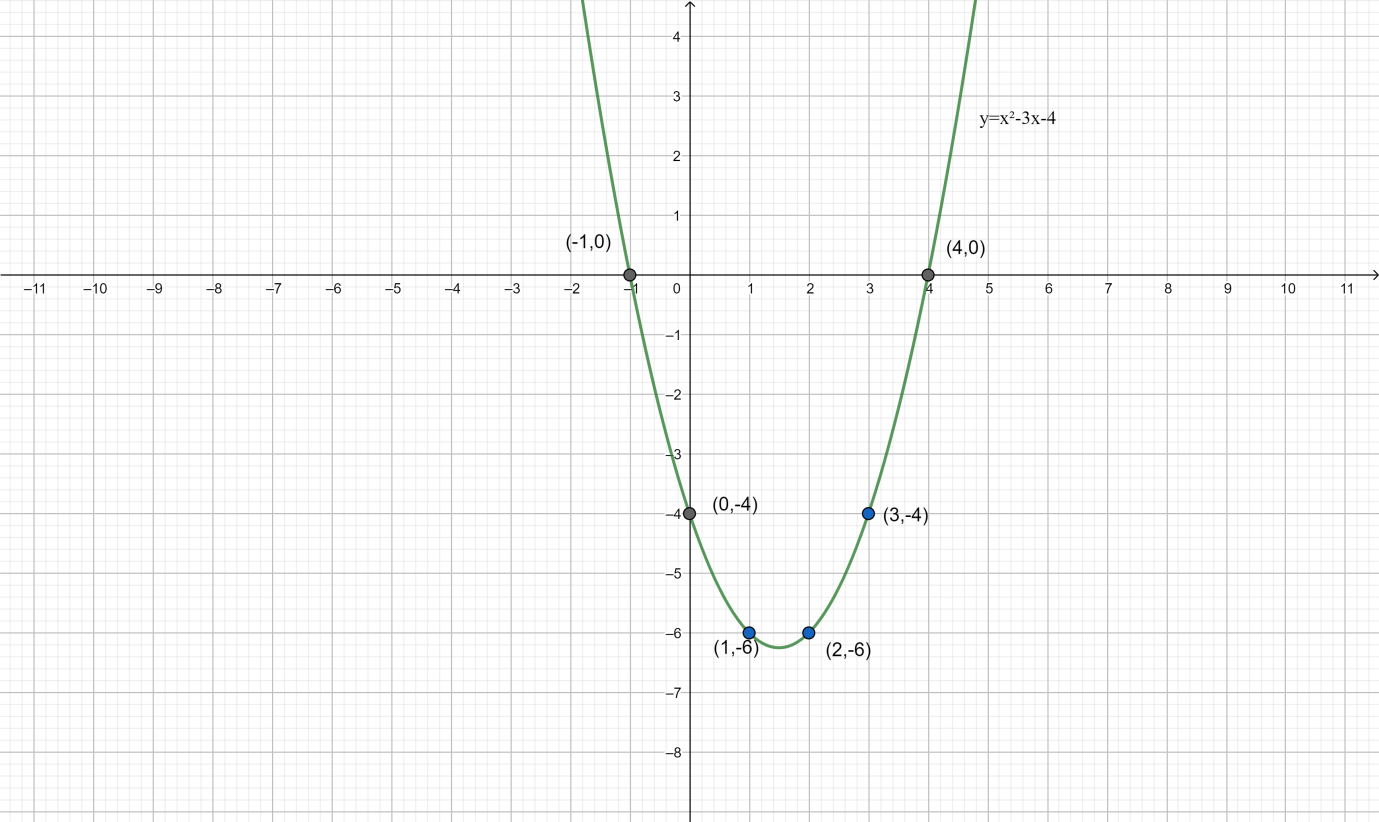We can easily conclude that the graphical representation of the given graph is a parabola.
Hence Graph drawn from the equation $$y=x^2-3x-4$$ will be a parabola.

Note: Parabola: A parabola is a U-shaped plane curve where any point is at an equal distance from a fixed point (known as the focus) and from a fixed straight line which is known as the directrix.
Coordinate: In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space.