
How do you graph \[\dfrac{1}{3}\] on a number line?
Answer
564k+ views
Hint: Here, we will graph the given number on the number line. We will find the decimal number for the given fraction and correct it to 4 decimal places. Then we will draw the number line and mark the decimal number on the line.
Complete step by step solution:
We are given a fraction \[\dfrac{1}{3}\].
Now, we will convert the given fractional number into a decimal number.
Let \[x\] be the given fraction number. So, we have \[x = \dfrac{1}{3}\].
Now, we will divide the numerator by the denominator of the given fraction to convert it into a decimal number. So, we get
\[ \Rightarrow x = 0.333....\]
\[ \Rightarrow x = 0.\overline 3 \]
Now, we will graph the number on a number line. So, we get
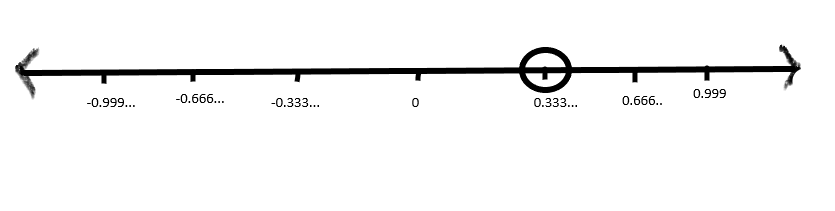
Therefore, the graph for the given number is represented on a number line.
Additional information:
We should know that the given number is a rational number since it is a non-terminating and recurring decimal. The bar over the decimal represents that the decimal is a recurring decimal. Recurring decimal is the repetition of decimal digits. Graphing a number on a number line is similar to the process of Visualization. This visualization is through successive magnification. We can visualize the representation of numbers on the number line by looking at a glimpse through a magnifying glass. The number line is a line similar only to \[x\]-axis with both the positive and negative integers.
Note:
We can also represent the fraction without converting the fraction into a decimal number. We should remember that the distance between two integers should be divided into the number of intervals as such the denominator. So, the interval is divided into 3 parts, since the denominator is 3. Thus, we will represent the number on a number line.
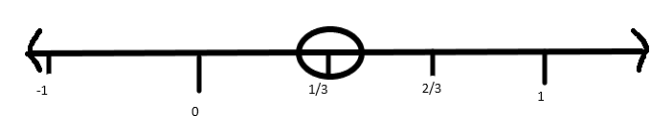
Complete step by step solution:
We are given a fraction \[\dfrac{1}{3}\].
Now, we will convert the given fractional number into a decimal number.
Let \[x\] be the given fraction number. So, we have \[x = \dfrac{1}{3}\].
Now, we will divide the numerator by the denominator of the given fraction to convert it into a decimal number. So, we get
\[ \Rightarrow x = 0.333....\]
\[ \Rightarrow x = 0.\overline 3 \]
Now, we will graph the number on a number line. So, we get

Therefore, the graph for the given number is represented on a number line.
Additional information:
We should know that the given number is a rational number since it is a non-terminating and recurring decimal. The bar over the decimal represents that the decimal is a recurring decimal. Recurring decimal is the repetition of decimal digits. Graphing a number on a number line is similar to the process of Visualization. This visualization is through successive magnification. We can visualize the representation of numbers on the number line by looking at a glimpse through a magnifying glass. The number line is a line similar only to \[x\]-axis with both the positive and negative integers.
Note:
We can also represent the fraction without converting the fraction into a decimal number. We should remember that the distance between two integers should be divided into the number of intervals as such the denominator. So, the interval is divided into 3 parts, since the denominator is 3. Thus, we will represent the number on a number line.

Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

Write a letter to the editor of the national daily class 7 english CBSE

Fill in the blanks with appropriate modals a Drivers class 7 english CBSE

What were the major teachings of Baba Guru Nanak class 7 social science CBSE

What are the controls affecting the climate of Ind class 7 social science CBSE





