
How do you graph and solve \[\left| x-4 \right| < 9\]?
Answer
543.3k+ views
Hint: We are given a question based on the absolute value inequalities. So, we will first remove the mod sign and that will give the range of the given expression. We will carry out calculations to get the equation in terms of \[x\] and get the range of \[x\]. And we will then map this range of \[x\] on the graph.
Complete step by step solution:
According to the given question, we are given an expression which we have to solve and graph it as well.
The given expression we have is,
\[\left| x-4 \right| < 9\]----(1)
We can see that the equation (1) has absolute value inequalities and that means the inequality assigned to the expression is not entirely correct. Because of the mod function used, the value if obtained directly will give a half-correct answer.
So, we have to remove the mod and take into consideration the possible range of the function,
That is,
\[\Rightarrow x-4 < \pm 9\]
\[\Rightarrow -9 < x-4 < 9\]----(2)
Now, we have the complete picture of the range of the given function. So, we will just have to rearrange equation (2) and write the expression for \[x\].
We will first add 4 to all sides of equation (2), we have,
\[\Rightarrow -9+4 < x-4+4 < 9+4\]
Solving the above expression, we get,
\[\Rightarrow -5 < x < 13\]
So, the value of \[x\] varies from -5 to 13, not including -5 and 13.
The graph of the above expression is as follows.
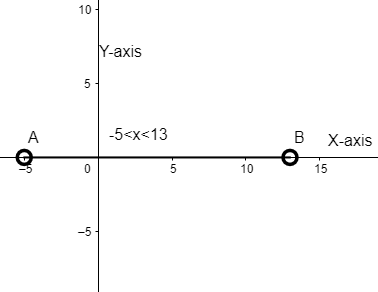
Note: In equation (2), we considered all the possibilities that expression can have else we would have got an incorrect answer. As we know that, \[\left| x \right|=3\], this would mean \[x=3\] or \[x=-3\]. Also, the range of \[x\] should be plotted correctly, since -5 and 13 are not included, it should be represented by hollow circles.
Complete step by step solution:
According to the given question, we are given an expression which we have to solve and graph it as well.
The given expression we have is,
\[\left| x-4 \right| < 9\]----(1)
We can see that the equation (1) has absolute value inequalities and that means the inequality assigned to the expression is not entirely correct. Because of the mod function used, the value if obtained directly will give a half-correct answer.
So, we have to remove the mod and take into consideration the possible range of the function,
That is,
\[\Rightarrow x-4 < \pm 9\]
\[\Rightarrow -9 < x-4 < 9\]----(2)
Now, we have the complete picture of the range of the given function. So, we will just have to rearrange equation (2) and write the expression for \[x\].
We will first add 4 to all sides of equation (2), we have,
\[\Rightarrow -9+4 < x-4+4 < 9+4\]
Solving the above expression, we get,
\[\Rightarrow -5 < x < 13\]
So, the value of \[x\] varies from -5 to 13, not including -5 and 13.
The graph of the above expression is as follows.
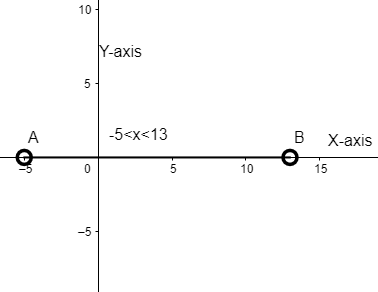
Note: In equation (2), we considered all the possibilities that expression can have else we would have got an incorrect answer. As we know that, \[\left| x \right|=3\], this would mean \[x=3\] or \[x=-3\]. Also, the range of \[x\] should be plotted correctly, since -5 and 13 are not included, it should be represented by hollow circles.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




