Question

Given,ABCD is a quadrilateral. Force $\vec {BA},\vec{BC},\vec{CD},\vec{DA}$ act at a point, their resultant is
\[\begin{align}
  & A.2\overrightarrow{AB} \\
 & B.2\overrightarrow{DA} \\
 & C.0 \\
 & D.\overrightarrow{2BA} \\
\end{align}\]

Answer 1

Hint: We know that we can find the resultant of any two given vectors from the parallelogram of vector addition, by moving the vectors if required such that they have a common point and the direction of the vectors are away from the point of contact.

Complete step by step solution:
Let us consider the quadrilateral ABCD as shown below,

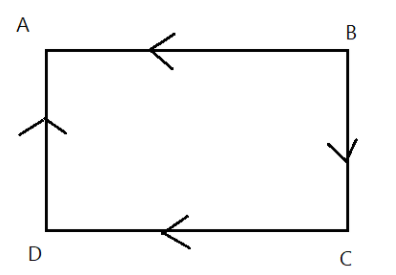
Since it is given that ABCD is a quadrilateral, we can say that $\vec AB+\vec BC+\vec CD+\vec DA=0$
Also, clearly, $\vec AB=-\vec BA$
Then we have
$\implies \vec BA=\vec BC+\vec CD+\vec DA$
From the given figure, we can say that $R=\vec BA+\vec BC+\vec CD+\vec DA$
$\implies R=\vec BA+\vec BA$
$\therefore R=2\vec BA$

Hence the correct answer is option \[D.\overrightarrow{2BA}\].

Additional information:
We know that vectors have both magnitude and direction. We also know that we can add, or multiply two given vectors.
Parallelogram law of vector addition states that the sum of the squares of all the sides of the parallelogram, give the squares of the two diagonals of the parallelogram. This law gives both the direction and the magnitude of the resultant vector.
Or, in simple terms the resultant vector due to the adjacent sides of a parallelogram, is the diagonal of the parallelogram.
The triangle law of vector addition is derived from the parallelogram of vector addition. Also, the parallelogram law of vector addition is often used in physics as most of the physical terms like force, work , tension and so on are vectors, and need to be added or subtracted often.

Note:
This sum may seem very hard at first glance, but if one draws the diagram and labels the diagram correctly, it is easy to solve the question. The question uses only the basic parallelogram law of vector addition and speed formula.