Question

Given two circles intersecting orthogonally having length of common chord $\dfrac{24}{5}$ units, the radius of one of the circles is 3 units. Angle between direct common tangents is \[\]
A. ${{\sin }^{-1}}\dfrac{24}{25}$\[\]
B. ${{\sin }^{-1}}\dfrac{4\sqrt{6}}{25}$\[\]
C. ${{\sin }^{-1}}\dfrac{4}{5}$\[\]
D. ${{\sin }^{-1}}\dfrac{12}{25}$\[\]

Answer 1

Hint: We denote the radius of smaller circle as ${{r}_{1}}$, the radius of larger circle as ${{r}_{2}}$, the half of the common chord as $d$ and the angle between common tangents as $\theta $. We use the fact that the line joining the center of two orthogonal circles will bisect the common chord and the angle between common tangents. Let $P, Q$ be centered, $LM$ is the common chord and $A, B$ points of contact of one common tangent. We draw AN parallel to PQ and prove $\angle BAN=\dfrac{\theta }{2}$. We find ${{r}_{2}}$ taking sine of angles in LPQ and given${{r}_{1}}=3,2d=\dfrac{24}{5}$. We find $\sin \dfrac{\theta }{2},\cos \dfrac{\theta }{2}$ and then use trigonometric identity $\sin 2A=2\sin A\cos A$.

Complete step-by-step solution

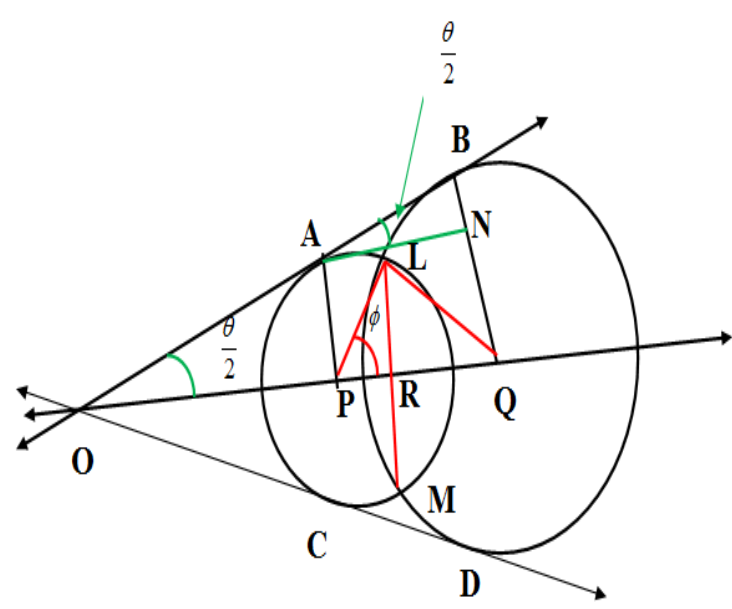
Let two orthogonal circles with centers P and Q intersect each other at points L and M. SO we have;
\[\angle PLQ=\angle PMQ={{90}^{\circ }}\]
The common chord is LM whose length is given in the question as $LM=\dfrac{24}{5}$.
Let the two $A,B$ and $C,D$ be the points of contact of the direct tangents at the same side. We know that the line joining the centre of two orthogonal circles will bisect the common chord and the angle between common tangents. Let us denote the point of intersection of common tangents O and the point of intersection of PQ and LM be R. Then we have
\[\begin{align}
  & \angle AOP=\angle COP=\dfrac{\theta }{2}\left( say \right) \\
 & LR=PR=d\left( say \right) \\
\end{align}\]
We have the radii of the circles
\[\begin{align}
  & PA=PL={{r}_{1}}\left( say \right) \\
 & QB=QL={{r}_{2}}\left( say \right) \\
\end{align}\]
We produce a parallel line from A with PQ which cuts BQ at N. Since radius is always perpendicular to tangent $\angle PAO=\angle PAB=\angle QBO={{90}^{\circ }}$. We have in triangle APO $\angle APO={{90}^{\circ }}-\dfrac{\theta }{2}$
So we have from using supplementary angles
\[\angle APQ={{180}^{\circ }}-\angle APO={{180}^{\circ }}-\left( {{90}^{\circ }}-\dfrac{\theta }{2} \right)={{90}^{\circ }}+\dfrac{\theta }{2}\]
We have parallel lines AN and PQ with the transverse lines AP. Then we have the adjacent angles
\[\begin{align}
  & \angle APQ+\angle APN={{180}^{\circ }} \\
 & \Rightarrow \angle APN={{180}^{\circ }}-\left( {{90}^{\circ }}+\dfrac{\theta }{2} \right)={{90}^{\circ }}-\dfrac{\theta }{2} \\
\end{align}\]
Now we have the complementary angles
\[\begin{align}
  & \angle PAB={{90}^{\circ }} \\
 & \Rightarrow \angle PAN+\angle BAN={{90}^{\circ }} \\
 & \Rightarrow \angle BAN={{90}^{\circ }}-\left( {{90}^{\circ }}-\dfrac{\theta }{2} \right)=\dfrac{\theta }{2} \\
\end{align}\]
Now let us consider the right angled triangle LPR. We have;
\[\sin \phi =\dfrac{LR}{PL}=\dfrac{d}{{{r}_{1}}}......\left( 1 \right)\]
We have in the right angled triangle LPQ $\angle LQP=\angle LQR={{90}^{\circ }}-\phi $. Now we consider the triangle LQR to have;
\[\begin{align}
  & \sin \left( {{90}^{\circ }}-\phi \right)=\dfrac{LR}{QL}=\dfrac{d}{{{r}_{2}}} \\
 & \Rightarrow \cos \phi =\dfrac{d}{{{r}_{2}}}.....\left( 2 \right) \\
\end{align}\]
We square and add corresponding sides of equation (1) and (2) to have;
\[\begin{align}
  & {{\sin }^{2}}\phi +{{\cos }^{2}}\phi =\dfrac{{{d}^{2}}}{{{r}_{1}}^{2}}+\dfrac{{{d}^{2}}}{{{r}_{2}}^{2}} \\
 & \Rightarrow 1={{d}^{2}}\left( \dfrac{{{r}_{1}}^{2}+{{r}_{2}}^{2}}{{{r}_{1}}^{2}{{r}_{2}}^{2}} \right) \\
 & \Rightarrow d=\dfrac{{{r}_{1}}{{r}_{2}}}{\sqrt{{{r}_{1}}^{2}+{{r}_{2}}^{2}}} \\
 & \Rightarrow 2d=\dfrac{2{{r}_{1}}{{r}_{2}}}{\sqrt{{{r}_{1}}^{2}+{{r}_{2}}^{2}}} \\
\end{align}\]
We have $LM=LR+PR=d+d=2d$ and it is given as $LM=\dfrac{24}{3}$. We are also given in the question${{r}_{1}}=3$. We use these values in above step to have;
\[\begin{align}
  & \Rightarrow LM=\dfrac{2\left( 3 \right){{r}_{2}}}{\sqrt{{{3}^{2}}+{{r}_{2}}^{2}}}=\dfrac{24}{5} \\
 & \Rightarrow \dfrac{{{r}_{2}}}{\sqrt{9+{{r}_{2}}^{2}}}=\dfrac{4}{5} \\
 & \Rightarrow 5{{r}_{2}}=4\left( \sqrt{9+{{r}_{2}}^{2}} \right) \\
 & \Rightarrow 25{{r}_{2}}^{2}=16\left( 9+{{r}_{2}}^{2} \right) \\
 & \Rightarrow 9{{r}_{2}}^{2}=16\times 9 \\
 & \Rightarrow {{r}_{2}}=4 \\
\end{align}\]
Let us consider the right angled triangle BAN we have;
\[\begin{align}
  & \sin \left( \dfrac{\theta }{2} \right)=\dfrac{BN}{AN} \\
 & \Rightarrow \sin \left( \dfrac{\theta }{2} \right)=\dfrac{BQ-NQ}{PQ} \\
 & \Rightarrow \sin \left( \dfrac{\theta }{2} \right)=\dfrac{BQ-AP}{PQ} \\
 & \Rightarrow \sin \left( \dfrac{\theta }{2} \right)=\dfrac{{{r}_{2}}-{{r}_{1}}}{PQ}....\left( 3 \right) \\
\end{align}\]
We use Pythagoras theorem in right angled triangle LPQ to have;
\[\begin{align}
  & P{{Q}^{2}}=P{{L}^{2}}+Q{{L}^{2}}={{r}_{1}}^{2}+{{r}_{2}}^{2} \\
 & \Rightarrow P{{Q}^{2}}={{3}^{2}}+{{4}^{2}} \\
 & \Rightarrow PQ=5 \\
\end{align}\]
We put the values of ${{r}_{1}}=3,{{r}_{2}}=4,PQ=5$ in (3) to have;
\[\begin{align}
  & \sin \left( \dfrac{\theta }{2} \right)=\dfrac{4-3}{5}=\dfrac{1}{5} \\
 & \Rightarrow \cos \dfrac{\theta }{2}=\sqrt{1-{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)}=\sqrt{1-{{\left( \dfrac{1}{5} \right)}^{2}}}=\sqrt{\dfrac{24}{25}}=\dfrac{2\sqrt{6}}{5} \\
 & \Rightarrow \sin \theta =\sin \left( 2\times \dfrac{\theta }{2} \right)=2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}=2\times \dfrac{1}{5}\times \dfrac{2\sqrt{6}}{5}=\dfrac{4\sqrt{6}}{25} \\
 & \Rightarrow \theta ={{\sin }^{-1}}\left( \dfrac{4\sqrt{6}}{25} \right) \\
\end{align}\]
So the correct option is B.

Note: We note that we have rejected negative square roots because distance can not be negative. Here we APQB as a parallelogram whose side AP is the distance between two centers of the orthogonal circles. The key in this problem is to show $\angle BAN=\dfrac{\theta }{2}$. We can alternatively solve it using the similarity of triangles BAN and BOQ.