Question

Given three points P, Q, R with \[P \equiv \left( {5,3} \right)\] and R lies on the x-axis. If equation of RQ is \[x - 2y = 2\] and PQ is parallel to the x-axis, then the centroid of \[\Delta PQR\] lies on the line:
A) \[2x + y - 9 = 0\]
B) \[x - 2y + 1 = 0\]
C) \[5x - 2y = 0\]
D) \[2x - 5y = 0\]

Answer 1

Hint: Here first we will find the coordinates of R using the equation of RQ then we will find the equation of PQ and then find the coordinates of Q as Q is the intersection point of PQ and QR and then we will finally use the formula of centroid of triangle to find the centroid.
The centroid of a triangle with coordinates of vertices as \[\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)\] is given by:-
\[x = \dfrac{{{x_1} + {x_2} + {x_3}}}{3}\] and \[y = \dfrac{{{y_1} + {y_2} + {y_3}}}{3}\]

Complete step-by-step answer:
               

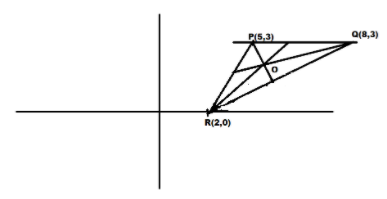
It is given that R lies on the x axis which implies y coordinate of R is zero.
Therefore, we will put \[y = 0\] in the given equation of RQ.
The given equation of RQ is:-
\[x - 2y = 2\]…………………………………..(1)
Putting \[y = 0\] we get:-
\[x - 2\left( 0 \right) = 2\]
Solving for x we get:-
\[
  x - 0 = 2 \\
   \Rightarrow x = 2 \\
 \]
Hence the coordinates of R are \[R\left( {2,0} \right)\]
Now it is given that PQ is parallel to x axis
Therefore, the equation of PQ is given by:-
\[y = 3\]……………………………(2)
Now we will find the coordinates of Q which is the intersection point of PQ and QR
Hence we need to solve the equations of PQ and QR in order to get point Q.
Putting the value from equation 2 in equation 1 we get:-
\[x - 2\left( 3 \right) = 2\]
Solving for x we get:-
\[
  x - 6 = 2 \\
   \Rightarrow x = 2 + 6 \\
   \Rightarrow x = 8 \\
 \]
And \[y = 3\] from equation 2
Hence the coordinates of Q are \[Q\left( {8,3} \right)\]
Hence the coordinates of the vertices of \[\Delta PQR\] are \[P \equiv \left( {5,3} \right)\], \[Q \equiv \left( {8,3} \right)\], \[R \equiv \left( {2,0} \right)\]
Now we know that the centroid of a triangle with coordinates of vertices as \[\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)\] is given by:-
\[x = \dfrac{{{x_1} + {x_2} + {x_3}}}{3}\] and \[y = \dfrac{{{y_1} + {y_2} + {y_3}}}{3}\]
Hence the centroid of \[\Delta PQR\] is given by:-
\[
  x = \dfrac{{5 + 8 + 2}}{3} \\
   \Rightarrow x = \dfrac{{15}}{3} \\
   \Rightarrow x = 5 \\
 \]
And,
\[
  y = \dfrac{{3 + 3 + 0}}{3} \\
   \Rightarrow y = \dfrac{6}{3} \\
   \Rightarrow y = 2 \\
 \]
Therefore centroid \[O \equiv \left( {5,2} \right)\]
Now since this point satisfies the equation \[2x - 5y = 0\]
Hence \[\left( {5,2} \right)\] lies on \[2x - 5y = 0\]

So, the correct answer is “Option D”.

Note: Students should note that the centroid of a triangle is the intersection point of medians drawn from each vertex to the opposite side. Also, students should note that when a line is parallel to x axis then its equation is in the form \[y = a\] and when a line is parallel to y axis then its equation is of the form \[x = a\]