Question

Given the point $(1,2)$ , find the equation on which it lies, how many such equations are there and draw the graph for one such equation.

Answer 1

Hint: The given point must be used in the form of graphical representation; you must consider the given data as an axis of a point and suit a variable to those values and then form an equation with respect to that variable.

Complete step-by-step solution:
Given data,
The point is given as, $(1,2)$,
Let assume the given point as $(x,y)$,
So, the point lies in the graph at $x = 1$ and $y = 2$.
The given axis that lies in the point is$(1,2)$,
Let $x = 1$,$y = 2$;
From the given point of the X axis and the Y axis, the possible equation which are formed is given as,
$x + y = 3$
$x - y = - 1$
$2x - y = 0$
From the given point in the question, we can able to form the greater number of the equation with help of the given points, by using the information of the points we can generate more equations, and the equation is drawn in the graph is given as,

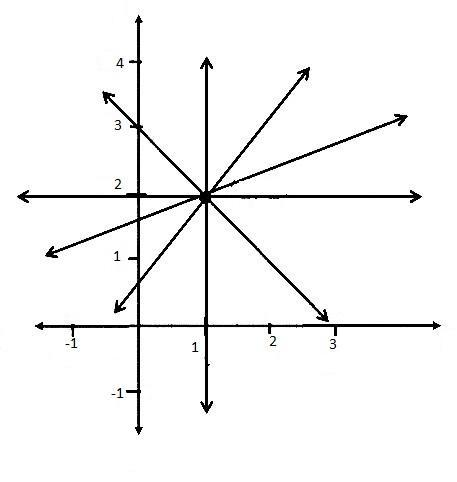
From the above graph, the lines which are passing through the point $\left( {1,2} \right)$ will form the greater number of the equations. And the equation which passes in the $x$ and $y$ may lead to the negative results.

Note: Substitute the value in $x$ and $y$ intercept ,we can also identify the slope, this can be done by calculating the slope between two known points of the line using the slope formula, for finding y intercept we must substitute the slope and coordinates of a point $(x,y)$ on the line in the slope intercept.