
Given the axis of a parabola lies along the x-axis. If its vertex and focus are at a distance 2 and 4 respectively from the origin on the positive x-axis, then which of the following points does not line on the parabola?
(a)
(b)
(c)
(d)
Answer
515.4k+ views
Hint: We start solving the problem by finding the equation of the axis of parabola. We use the fact that vertex and focus lie on the axis of parabola to find and calculate them. We find the distance between vertices and focus to find the equation of the parabola. Once we find the equation of parabola, we substitute the points present in options to get the required answer.
Complete step-by-step answer:
According to the problem, the axis of the parabola lies along the x-axis and its vertex and focus area at a distance of 2 and 4 units respectively from the origin on the positive axis. We need to find which of the points given in options are not on the parabola.
We know that the equation of x-axis is
Since, the vertex of the parabola is 2 units from the origin in the positive direction of the x-axis and we know that the vertex lies on the axis of the parabola. So, we get the x-co-ordinate of the vertex as 2.
We get the vertex at the point
Since, the focus of the parabola is 4 units from the origin in the positive direction of x-axis and we know that the focus lies on the axis of the parabola. So, we get the x-co-ordinate of the focus as 4.
We get the vertex at the focus
Let us find the distance between the vertex and focus of the parabola. We know that distance between two points
The distance between Vertex and focus is
We know that equation of the parabola whose axis is
So, we get the equation of the parabola as
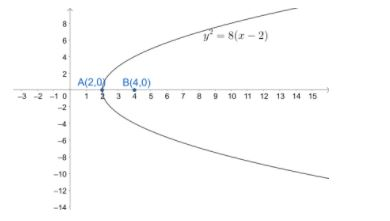
Let us substitute
The point
Let us substitute
The point
Let us substitute
The point
Let us substitute
The point
We have found that the point
So, the correct answer is “Option C”.
Note: We should not confuse the equation of x-axis with x=0 which leads to the wrong solution. We should know that the distance between focus and vertex is 4 times the length of the latus rectum of parabola. We should know that the parabola is symmetric about its axis. Similarly, we can expect problems to find the equation of tangent at a given point after finding the equation.
Complete step-by-step answer:
According to the problem, the axis of the parabola lies along the x-axis and its vertex and focus area at a distance of 2 and 4 units respectively from the origin on the positive axis. We need to find which of the points given in options are not on the parabola.
We know that the equation of x-axis is
Since, the vertex of the parabola is 2 units from the origin in the positive direction of the x-axis and we know that the vertex lies on the axis of the parabola. So, we get the x-co-ordinate of the vertex as 2.
We get the vertex at the point
Since, the focus of the parabola is 4 units from the origin in the positive direction of x-axis and we know that the focus lies on the axis of the parabola. So, we get the x-co-ordinate of the focus as 4.
We get the vertex at the focus
Let us find the distance between the vertex and focus of the parabola. We know that distance between two points
The distance between Vertex and focus is
We know that equation of the parabola whose axis is
So, we get the equation of the parabola as

Let us substitute
The point
Let us substitute
The point
Let us substitute
The point
Let us substitute
The point
We have found that the point
So, the correct answer is “Option C”.
Note: We should not confuse the equation of x-axis with x=0 which leads to the wrong solution. We should know that the distance between focus and vertex is 4 times the length of the latus rectum of parabola. We should know that the parabola is symmetric about its axis. Similarly, we can expect problems to find the equation of tangent at a given point after finding the equation.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
The flightless birds Rhea Kiwi and Emu respectively class 11 biology CBSE

1 litre is equivalent to A 1000mL B 100cm3 C 10mL D class 11 physics CBSE

A car travels 100 km at a speed of 60 kmh and returns class 11 physics CBSE

Name the Largest and the Smallest Cell in the Human Body ?

Explain zero factorial class 11 maths CBSE

In tea plantations and hedge making gardeners trim class 11 biology CBSE




